apresmidi.html

Il est formellement interdit de quitter la salle avant la fin de l'épreuve .

Aucun document n'est autorisé, la calculatrice n'est pas autorisée.

Sur l'ordinateur mis à service, seul le logiciel " maple " est utilisable : internet et intranet sont mis hors service, les moyens de communication sont coupés (mail, telnet, ...), la sauvegarde ainsi que l'accès aux documents personnel sont également exclus.

Le téléphone portable est évidemment interdit aussi.

Le compte-rendu est à rendre uniquement sur copie et manuscrit : pas de sortie imprimante.

Exercice 1 (trois points)

Soit une popuation P prise au hasard.

Soit la proportion de fumeurs à l'étape n dans la population P ; est donc la proportion de non-fumeurs à l'étape n dans la population P .

On considère qu'un fumeur de cette population P à l'étape n a une probabilité de de rester fumeur à l'étape (et donc une probabilité de de devenir non-fumeur à l'étape ). Qui plus est, on considère qu'un non-fumeur de cette population P à l'étape n a une probabilité de de rester non-fumeur à l'étape (et donc une probabilité de de devenir fumeur à l'étape ).

On a donc ou encore .

On suppose que .

a) Donner en fonction de n .

b) Donner la limite l de la suite ( ) lorsque n tend vers .

c) Si on modifie la valeur de , la valeur de l est-elle modifiée ?

> restart:

> rsolve({p(n+1)=7/10*p(n)+1/10,p(0)=1/2},p(n));

> p:=n->1/6*(7/10)^n+1/3;

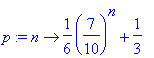
> limit(p(n),n=infinity);

> rsolve({q(n+1)=7/10*q(n)+1/10},q(n));

> q:=n->q[0]*(7/10)^n-1/3*(7/10)^n+1/3;

> limit(q(n),n=infinity);

... la limite n'est donc pas modifiée si on modifie la valeur de .

Exercice 2 (cinq points)

Soit p une fonction polynôme telle que .

On impose au polynôme p d'avoir deux racines réelles distinctes.

a) Quelle condition cela impose-t-il à m ?

b) Pour quelle(s) valeur(s) de m la somme des carrés des racines du polynôme p vaut-elle 6 ?

> restart:

> p:=x->x^2+m*(x+1)+1;

> sol:=solve(p(x)=0,x);

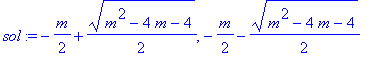
> solve(m^2-4*m-4>0,m);

a) D'où m est soit plus petit que , soit plus grand que .

> solve(sol[1]^2+sol[2]^2=6,m);

b) m=4 ou m=-2.

> is(4>2+2*2^(1/2));is(4<2-2*2^(1/2));

> is(-2>2+2*2^(1/2));is(-2<2-2*2^(1/2));

Ainsi, la seule valeur de m qui satisfait les deux conditions est -2.

Exercice 3 (cinq points)

Soit la suite ( ) définie par récurrence pour et .

On définit alors une suite ( ) par pour .

a) Donner en fonction de .

b) En déduire en fonction de n.

c) Puis, enfin en fonction de n .

> restart:
f:=x->-2*(x+6+sqrt(5)*x-2*sqrt(5))/(-3*x-2+sqrt(5)*x-2*sqrt(5)):
g:=x->(x-2)/(x+2):solve(g(x)=y,x);

> ginverse:=y->-2*(1+y)/(-1+y):

> u[n]:=ginverse(v[n]):u[n+1]:=simplify(f(u[n])):v[n+1]:=simplify(g(u[n+1]));#donne v[n+1] en fonction de v[n]

> V(0):=g(1):rsolve(V(n+1)=1/2*V(n)*(-1+5^(1/2)),V(n));#donne v[n] en fonction de n

> simplify(ginverse(-1/3*(-1/2+1/2*5^(1/2))^n));

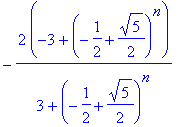
Exercice 4 (sept points)

Source : "Les Reid – Problem Corner – South West Missouri University".

a) Chercher x , y et z des entiers naturels non nuls tels que .

b) Chercher x , y et z des entiers naturels non nuls tels que .

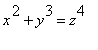c) Chercher x , y et z des entiers naturels non nuls tels que .

d) Donner une procédure "maple" qui donne, si c'est possible, tous les triplets (x, y, z) d'entiers naturels non nuls tels que , avec x < y < z et x , y et z tous trois inférieurs strictement à 100 .

e) Donner une procédure "maple" qui donne, si c'est possible, tous les triplets (x, y, z) d'entiers naturels non nuls tels que , avec x < y < z et x , y et z tous trois inférieurs strictement à 100 .

Pour le a), pas besoin de maple, mais on modifiera le programme ensuite pour qu'il fonctionne pour le b) et le c).

> restart:

> NN:=2:# Ce sera une majoration pour le z. On l'augmente petit à petit ...
L:=NULL:
for x from 1 to floor(NN^3) do
for y from 1 to floor(NN^(3/2)) do
for z from 1 to NN do
if x+y^2=z^3 then L:=L,[x,y,z] fi: od:od:od:

> L;

> restart:

> NN:=6:# Ce sera une majoration pour le z. On l'augmente petit à petit ...
L:=NULL:
for x from 1 to floor(NN^2) do
for y from 1 to floor(NN^(4/3)) do
for z from 1 to NN do
if x^2+y^3=z^4 then L:=L,[x,y,z] fi: od:od:od:

> L;

> restart:

> NN:=32:# Ce sera une majoration pour le z. On l'augmente petit à petit ...
L:=NULL:
for x from 1 to floor(NN^(5/3)) do
for y from 1 to floor(NN^(5/4)) do
for z from 1 to NN do
if x^3+y^4=z^5 then L:=L,[x,y,z] fi: od:od:od:

> L;

> L:=NULL:# on y stocke les solutions au problème d)
for x from 1 to 100 do
for y from x to 100 do
for z from y to 100 do
if x^2+y^2=z^2 then L:=L,[x,y,z] fi:
od:od:od:L;

> L:=NULL:# on y stocke les solutions au problème e)
for x from 1 to 100 do
for y from x to 100 do
for z from y to 100 do
if x^3+y^3=z^3 then L:=L,[x,y,z] fi:
od:od:od:L;

C'est le "last Fermat theorem" qui prouve qu'il n'y a pas de solution à ce problème e).

> Fin (Philippe RYCKELYNCK & Denis VEKEMANS);

Error, missing operator or `;`