examen.html

Il est obligatoire d'être présent au début de l'épreuve .

Il est formellement interdit de quitter la salle avant la fin de l'épreuve .

La durée de l'épreuve est de 2 heures.

Aucun document n'est autorisé, la calculatrice n'est pas autorisée.

Sur l'ordinateur mis à service, seul le logiciel " maple " est utilisable : internet et intranet sont mis hors service, les moyens de communication sont coupés (mail, telnet, ...), la sauvegarde ainsi que l'accès aux documents personnel sont également exclus.

Le téléphone portable est évidemment interdit aussi.

Le compte-rendu est à rendre uniquement sur copie et manuscrit : pas de sortie imprimante, pas d'enregistrement de fichier.

> restart:

Questions de cours .

1) Donner des coefficients a , b , et c réels tels que .

2) Donner les solutions de l'équation différentielle .

> expand(cos(5*x));

> dsolve(diff(diff(f(x),x),x)+f(x)=cos(x)+x*sin(x),f(x));

Questions de cours .

1) Donner le polynôme p tel que .

2) Donner la primitive de .

> simplify((x^8-2*x^2+1)/(x^2-1));

> f:=x->(x^3+x^2+x+1)*(exp(x));int(f(x),x);

> restart:

Exercice 1 . Géométrie affine.

Soit P1, P2 et P3 trois points du plan.

On considère le triangle T donné par ses sommets P1, P2 et P3.

Compléter la procédure ci-dessous pour qu'elle affirme ou infirme le fait que le triangle T soit isocèle.

> triangleisocele:=proc(P1,P2,P3)
local L1,L2,L3,Q1,Q2,Q3;
Q1:=P3-P2:
Q3:=P2-P1:
Q2:=P1-P3:
L1:=simplify(sqrt(Q1[1]^2+Q1[2]^2)):
L3:=simplify(sqrt(Q3[1]^2+Q3[2]^2)):
L2:=simplify(sqrt(Q2[1]^2+Q2[2]^2)):
if L1=L2 then RETURN(`le triangle est isocèle en `,P3) fi:
if L2=L3 then RETURN(`le triangle est isocèle en `,P1) fi:
if L3=L1 then RETURN(`le triangle est isocèle en `,P2) fi:
RETURN(`le triangle n'est pas isocèle`)
end;

> P1:=[0,0]:P2:=[3,1]:P3:=[2,2]:
triangleisocele(P1,P2,P3);

> P1:=[0,0]:P2:=[3,1]:P3:=[0,2]:
triangleisocele(P1,P2,P3);

> restart:

Exercice 1 . Géométrie affine.

Soit P1, P2, P3 et P4 quatre points du plan.

On considère le quadrilatère Q donné par ses sommets consécutifs

P1, P2, P3 et P4.

Compléter la procédure ci-dessous pour qu'elle affirme ou infirme le fait que le quadrilatère Q soit un trapèze.

> trapeze:=proc(P1,P2,P3,P4)
local P12,P23,P34,P41;
P12:=P1-P2:
P23:=P2-P3:
P34:=P3-P4:
P41:=P4-P1:
if P12[1]/P34[1]=P12[2]/P34[2] then RETURN(`le quadrilatère est un trapèze et la droite (`,P1,P2,`) est parallèle à la droite (`,P3,P4,`)`) fi:
if P23[1]/P41[1]=P23[2]/P41[2] then RETURN(`le quadrilatère est un trapèze et la droite (`,P1,P4,`) est parallèle à la droite (`,P2,P3,`)`) fi:
RETURN(`le quadrilatère n'est pas un trapèze`)
end;

> P1:=[0,0]:P2:=[3,1]:P3:=[2,2]:P4:=[3,3]:
trapeze(P1,P2,P3,P4);

> P1:=[0,0]:P2:=[3,1]:P3:=[0,2]:P4:=[3,3]:
trapeze(P1,P2,P3,P4);

> restart:

Exercice 2 . Fonctions de chiffres.

Chercher un nombre naturel de la forme 1a234b567c89 (en base 10 , 9 est chiffre des unités, 8 est chiffre des dizaines, ... et 1 est chiffre des centaines de milliards) qui soit multiple de 77 .

Combien existe-t-il de nombres de la fome 1a234b567c89 qui soient multiples de 77 ?

> L:=NULL:
for a from 0 to 9 do
for b from 0 to 9 do
for c from 0 to 9 do
N:=102340567089+100*c+1000000*b+10000000000*a; if irem(N,77)=0 then L:=L,N fi:
od:
od:
od:
L:=[L];nops(L);

> restart:

Exercice 2 . Fonctions de chiffres.

Chercher un nombre de la forme abcd ( a est chiffre des milliers supposé non nul, b est chiffre des centaines, c est chiffre des dizaines et d est chiffre des unités) qui soit égal à .

> L:=NULL:
for a from 1 to 9 do
for b from 0 to 9 do
for c from 0 to 9 do
for d from 0 to 9 do
N:=1000*a+100*b+10*c+d; if N=a^5+b^4+c^3+d^2 then L:=L,N fi:
od:
od:
od:
od:
L:=[L];nops(L);

> restart:

Exercice 3 . Fonctions d'une variable réelle à valeurs réelles.

Quelle est l'utilité de la procédure suivante ?

Remarque : a , b et précision sont des nombres réels ; f est une fonction d'une variable réelle à valeurs réelles.

> dichotomie:=proc(f,précision,a,b)
local A,B;
if a>=b then ERROR(`a doit être strictement plus petit que b`) fi:
if f(a)*f(b)>0 then ERROR(`f ne change pas forcément de signe sur [a,b]`) fi:
A:=a:B:=b:
while B-A>=précision do
if f(A)*f((A+B)/2)<0 then B:=(A+B)/2 else A:=(A+B)/2 fi:od:
RETURN((A+B)/2)
end:

> f:=x->x^2-2;evalf(dichotomie(f,.000001,0,2));

Cette procédure recherche une solution de l'équation f(x)=0 par la méthode dite de dichotomie : en algorithmique, la dichotomie (« couper en deux » en grec) est un processus itératif ou récursif de recherche où, à chaque étape, l'espace de recherche est restreint à l'une des deux parties.

Connaissez-vous une autre façon d'obtenir le même résultat avec maple lorsqu'on considère la fonction ?

> fsolve(x^2-2,x);

> restart:

Exercice 3 . Fonctions d'une variable réelle à valeurs réelles.

Quelle est l'utilité de la procédure suivante ?

Remarque : a , b et précision sont des nombres réels ; f est une fonction polynômiale d'une variable réelle à valeurs réelles.

> solutionevidente:=proc(f)
local a,b,c,d,L,M;
L:=NULL:
for a from -5 to 5 do
for b from -5 to 5 do
for c from 1 to 5 do
for d from 1 to 5 do
if simplify(f((a+b*sqrt(c))/d))=0 then L:=L union {(a+b*sqrt(c))/d} fi:
od:od:od:od:
RETURN(L)
end:

> p:=x->x^2-x-1;solutionevidente(p);

${1/2+1/2*5^(1/2), 1/2-1/2*5^(1/2)}$

Ce programme recherche des solutions "évidentes" de l'équation sous la forme avec a entier compris entre -5 et 5, b entier compris entre -5 et 5, c entier compris entre 1 et 5 et d compris entre 1 et 5.

Connaissez-vous une autre façon d'obtenir le même résultat avec maple lorsqu'on considère le polynôme ?

> solve(p(x)=0,x);

> restart:

Exercice 4 . Algèbre linéaire.

a est un paramètre réel. Soit , soit et soit .

Pour quelle(s) valeur(s) de a , la matrice A est-elle inversible ?

Lorsque A est inversible, donner la matrice inverse de A .

Lorsque A n'est pas inversible, selon la valeur de a , donner l'image et le noyau de A .

Soit le système d'équations AX=B .

Lorsque A est inversible, X est définie de façon unique par . Donner la matrice X .

Lorsque A n'est pas inversible, selon la valeur de a , donner l'ensemble des matrices X répondant à la question.

Exercice 4 . Algèbre linéaire ( version pour les GSI ).

Résoudre le système d'équations ${a*x+a^2*y+a^3*z = 2, a*x-y+4*a*z = a, x+a*y+2*a*z = 1}$ dans les trois cas suivants

a=0
a=2
et .

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> A:= matrix([[a, a^2, a^3], [a, -1, 4*a], [1, a, 2*a]]);X:= matrix([[x], [y], [z]]);B:= matrix([[2], [a], [1]]);

> Ainv:=factor(inverse(A));

> solve(-2+a-2*a^2+a^3=0,a);#Lorsque a=0 ou lorsque a=2, la matrice A n'est pas inversible.

> simplify(multiply(Ainv,B));

> a:=0:A:= matrix([[a, a^2, a^3], [a, -1, 4*a], [1, a, 2*a]]);X:= matrix([[x], [y], [z]]);B:= matrix([[2], [a], [1]]);

> colspace(A);#image de A
nullspace(A);#noyau de A

> solve({a*x+a^2*y+a^3*z=2,a*x-y+4*a*z=a,x+a*y+2*a*z=1},{x,y,z});

Cas a=0. Pour la résolution du système linéaire, la première ligne de AX est 0 et la première ligne de B est 2 . Il n'y a donc pas de solution dans ce cas à AX=B .

> a:=2:A:= matrix([[a, a^2, a^3], [a, -1, 4*a], [1, a, 2*a]]);X:= matrix([[x], [y], [z]]);B:= matrix([[2], [a], [1]]);

> colspace(A);#image de A
nullspace(A);#noyau de A

> solve({a*x+a^2*y+a^3*z=2,a*x-y+4*a*z=a,x+a*y+2*a*z=1},{x,y,z});

Cas a=2. Si z est quelconque, y=0 et x=1-4z.

Version pour les GSI.

> restart:
solve({a*x+a^2*y+a^3*z=2,a*x-y+4*a*z=a,x+a*y+2*a*z=1},{x,y,z});

${z = -1/(a^2), x = 1/a*(2+5*a+a^3)/(a^2+1), y = 2/a*(-2+a)/(a^2+1)}$

> a:=0:solve({a*x+a^2*y+a^3*z=2,a*x-y+4*a*z=a,x+a*y+2*a*z=1},{x,y,z});

Cas a=0. Il n'y a pas de solution.

> a:=2:solve({a*x+a^2*y+a^3*z=2,a*x-y+4*a*z=a,x+a*y+2*a*z=1},{x,y,z});

Cas a=2. Si z est quelconque, y=0 et x=1-4z.

> restart:

Exercice 4 . Algèbre linéaire.

a est un paramètre réel. Soit .

Pour quelle(s) valeur(s) de a et b , la matrice M est-elle inversible ?

Lorsque M est inversible, donner la matrice inverse de M .

Lorsque M n'est pas inversible, selon la valeur de a , donner l'image et le noyau de M .

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> M:= matrix([[1, 1, 1, 1, 1], [1, 1, 1, 1, a], [1, 1, 1, a, a^2], [1, 1, a, a^2, a^3], [1, a, a^2, a^3, a^4]]);

> inverse(M);

> a:=1:M:= matrix([[1, 1, 1, 1, 1], [1, 1, 1, 1, a], [1, 1, 1, a, a^2], [1, 1, a, a^2, a^3], [1, a, a^2, a^3, a^4]]);

> colspace(M);#image de A
nullspace(M);#noyau de A

> restart:

Exercice 5 . Minimisation d'une aire.

Soit (O, i , j ) un repère orthonormé.

On considère l'ensemble des points M ( ) pour x variant entre 0 et 1 .

1) Soit la tangente en M à l'ensemble . Donner l'équation de la tangente .

2) La tangente coupe l'axe ( O i ) en un point A et l'axe ( O j ) en un point B . Donner les coordonnées des points A et B .

3) Donner l'aire du triangle OAB en fonction de x .

4) Donner la valeur (ou les valeurs) de x pour que le triangle OAB ait une aire extrémale.

5) Donner la valeur (ou les valeurs) de x pour que le triangle OAB ait une aire minimale.

> f:=x->1-x^2;
M:=[x,f(x)];#coordonnées de M
T:=X->diff(f(x),x)*(X-x)+f(x);#la fonction T donne l'équation de la tangente à la courbe en M
solve(T(X)=0,X);#abscisse du point A
A:=[1/2*(x^2+1)/x,0];
T(0);#ordonnée du point B
B:=[0,x^2+1];
Aire:=x->(1/2*(x^2+1)/x)*(x^2+1)/2;#la fonction Aire donne l'aire du triangle OAB en fonction de x
diff(Aire(x),x);
solve(diff(Aire(x),x)=0,x);#les points critiques sont en 0 (bord gauche), en 1 (bord droit), et en 1/3*3^(1/2) ;
limit(Aire(x),x=0,right);#en 0, la limite est +infinity ;
limit(Aire(x),x=1);#en 1, la valeur est 1 ;
Aire(1/3*3^(1/2));#en 1/3*3^(1/2), la valeur de l'Aire est 4/9*3^(1/2) et le tableau de variations nous permet de conclure qu'il s'agit d'un minimum.

Exercice 5 . Minimisation d'une durée.

Soit ( O , i , j ) un repère orthonormé.

Soit A (15,0), M ( x ,0) et B (0,9) ( x est compris entre 0 et 15).

Un individu (c'est-à-dire un point) parcourt le trajet composé de la réunion des segments [ AM ] et [ MB ], de A vers B .

L'individu se déplace sur le segment [ AM ] à la vitesse de 5 par heure et sur le segment [ MB ] à la vitesse de 4 par heure.

1) Exprimer la distance AM en fonction de x . Déterminer le temps de parcours sur le segment [ AM ] en fonction de x .

2) Exprimer la distance MB en fonction de x . Déterminer le temps de parcours sur le segment [ MB ] en fonction de x .

3) Donner le temps de parcours total en fonction de x .

4) Donner la valeur (ou les valeurs) de x pour que le temps de parcours total soit extrémal.

5) Donner la valeur (ou les valeurs) de x pour que le temps de parcours total soit minimal.

> AM:=x->15-x;#la fonction AM donne la distance AM
tAM:=x->(15-x)/5;#la fonction tAM donne le temps de parcours du segment [AM]
MB:=x->sqrt(81+x^2);#la fonction MB donne la distance MB
tMB:=x->sqrt(81+x^2)/4;#la fonction tMB donne le temps de parcours du segment [MB]
t:=x->tAM(x)+tMB(x);#la fonction t donne le temps de parcours sur le trajet complet
solve(diff(t(x),x)=0);#les points critiques sont en 0 (bord gauche), en 15 (bord droit), et en 12 ;
limit(t(x),x=0,right);#en 0, la limite est 21/4 ;
limit(t(x),x=15);#en 15, la valeur est 3/4*34^(1/2) ;
t(12);#en 12, la valeur de t est 87/20 et le tableau de variations nous permet de conclure qu'il s'agit d'un minimum.

> restart:

Exercice 6 .On considére la fonction suivante

(a) Donnez un tableau de variations de cette fonction avec "maple" ainsi qu'un tracé sur un intervalle significatif.

(b) Peut-on trouver exactement une primitive de la fonction racine carrée de f(x) ?

et en donner une valeur approchée à 8 chiffres.

> f:=x-> exp(-2*x)+exp(-x)+ 3;
diff(f(x),x);
plot(f(x),x=-1..4);
Int(sqrt(f(x)),x)=int(sqrt(f(x)),x);
Int(1/f(x),x=0..1)=int(1/f(x),x=0..1);
evalf(int(1/f(x),x=0..1));

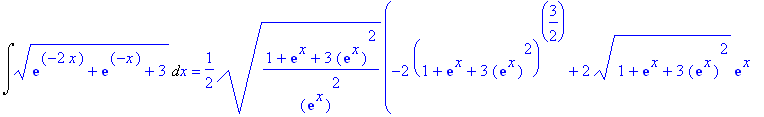
> restart:

Exercice 6 . Formule de John Machin.

Cet exercice idéalement devrait être fait aussi à la main, comme en 1705.... On demande seulement des justifications avec "maple" .

(a) Donner un intervalle de R sur lequel la fonction tangente est injective.

(b) Rappeler la définition de la fonction arctangente.

(d) Donner un tracé dela fonction arctangente.

(e) Rappeler la formule donnant tan(a+b).

(f) Soient les nombres = et = .

- Donner une valeur approchée de , puis de .

- Montrer que et déduire que .

Grace à cette formule et au développement limité de la fonction (Grégory), John Machin fut le premier à obtenir les 100 premières décimales de .

De , on déduit

- le développement limité à l'ordre 1 donne alors : proche de ou encore proche de .

- le développement limité à l'ordre 3 donne alors : proche de ou encore proche de .

(g) Que donne le développement limité à l'ordre 5 comme approximation de ?

> f:=x->tan(x);
plot(f(x),x=-Pi/2+.2..Pi/2-.2);#tan est bijective sur ]-Pi/2,Pi/2[

> g:=x->arctan(x);
D(g)(x);

> plot(g(x),x=-5..5);

> expand(tan(a+b));

> alpha:= Pi/4+arctan(1/239); beta:= 4*arctan(1/5);

> expand(tan(alpha));expand(tan(beta));simplify(tan(alpha)-tan(beta));

> for a from 2 to 10 by 2 do subs(x=1/5,convert(16*series(arctan(x),x=0,a),polynom))-subs(x=1/239,convert(4*series(arctan(x),x=0,a),polynom)),evalf(subs(x=1/5,convert(16*series(arctan(x),x=0,a),polynom))-subs(x=1/239,convert(4*series(arctan(x),x=0,a),polynom)))
od;

> series(arctan(x),x,12);#les coefficients du développement limité sont facilement mémorisables et calculables ; le fait que cette série soit alternée assure que deux approximants consécutifs constituent un encadrement de la valeur de Pi.

> Fin (Philippe RYCKELYNCK & Denis VEKEMANS)

Error, missing operator or `;`