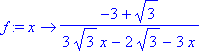
EXERCICE 1
| > | restart: |
En considérant la fonction f ,
| > | f:=x->(-3+3^(1/2))/(3*3^(1/2)*x-2*3^(1/2)-3*x); |
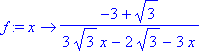
on a
| > | u[n+1]=f(u[n]); |
![u[n+1] = (-3+3^(1/2))/(3*3^(1/2)*u[n]-2*3^(1/2)-3*u[n])](partiel2008_mercredi/partiel2008_mercredi2.gif)
On nous demande de vérifier que la suite
![]() est géométrique ...
est géométrique ...
A l'aide de la fonction g,
| > | g:=x->(-1+sqrt(3)*x)/(x-1); |
![]()
on a
| > | v[n+1]=g(u[n+1]);v[n]=g(u[n]); |
![v[n+1] = (-1+3^(1/2)*u[n+1])/(u[n+1]-1)](partiel2008_mercredi/partiel2008_mercredi5.gif)
![v[n] = (-1+3^(1/2)*u[n])/(u[n]-1)](partiel2008_mercredi/partiel2008_mercredi6.gif)
On manipule alors l'équation
![]() qui équivaut successivement à
qui équivaut successivement à
![]() puis à
puis à
![]() où h est la fonction réciproque de fonction g, si celle-ci existe ... pour obtenir
où h est la fonction réciproque de fonction g, si celle-ci existe ... pour obtenir
![]() en fonction
en fonction
![]() .
.
On recherche la fonction réciproque de la fonction g :
| > | solve(g(x)=y,x); |
![]()
et donc
| > | h:=y->(-1+y)/(-3^(1/2)+y); |
![]()
puis il ne reste plus qu'à simplifier l'expression
![]() pour obtenir
pour obtenir
![]() ...
...
| > | simplify(g(f(h(v[n])))); |
![-1/3*v[n]*(-3+3^(1/2))/(-1+3^(1/2))](partiel2008_mercredi/partiel2008_mercredi16.gif)
| > | evalf(-1/3*v[n]*(-3+3^(1/2))/(-1+3^(1/2))); |
![]()
Ainsi,
![v[n+1] = -(-3+sqrt(3))/(3*(-1+sqrt(3)))*v[n]](partiel2008_mercredi/partiel2008_mercredi18.gif) et la suite
et la suite
![]() est arithmétique de raison
est arithmétique de raison
 . Remarque :
. Remarque :
![]() est une autre expression de cette raison. On obtient ainsi
est une autre expression de cette raison. On obtient ainsi
| > | v[n]:=(-1/3*(-3+3^(1/2))/(-1+3^(1/2)))^n*v[0]; |
![v[n] := (-1/3*(-3+3^(1/2))/(-1+3^(1/2)))^n*v[0]](partiel2008_mercredi/partiel2008_mercredi22.gif)
puis
| > | u[n]:=simplify(h(v[n])); |
![u[n] := ((1-1/3*3^(1/2))^n*v[0]-(-1+3^(1/2))^n)/(-3^(1/2)*(-1+3^(1/2))^n+(1-1/3*3^(1/2))^n*v[0])](partiel2008_mercredi/partiel2008_mercredi23.gif)
Conclusion : la suite
![]() est convergente (sa limite est nulle) et la suite
est convergente (sa limite est nulle) et la suite
![]() est convergente (sa limite est
est convergente (sa limite est
![]() ).
).
Remarque : vous aurez reconnu l'exercice 6 de la séance 1.
EXERCICE 2
| > | restart: |
Warning, the protected name order has been redefined and unprotected
Il s'agit ici de chercher dans l'ensemble {100, 101, 102, ..., 999} ceux qui sont abondants (on les dénombre avec le compteur a ) et ceux qui sont déficients (on les dénombre avec le compteur d ). Remarque : les nombres qui ne sont ni abondants, ni déficients sont parfaits.
| > | f := x->-exp(-x)+2*exp(x); solve(f(x)=y,x); |
![]()

La bijection réciproque est donc
 , car la quantité
, car la quantité
 étant toujours négative, son logarithme népérien n'est pas réel.
étant toujours négative, son logarithme népérien n'est pas réel.
| > | g:=y->-ln(-y/2+sqrt(y^2+8)/2); plot({f(x),g(x),x},x=-1..1); |
![]()
![[Maple Plot]](partiel2008_mercredi/partiel2008_mercredi32.gif)
Ainsi, le nombre de nombres abondants entre 100 et 999 est 224 et le nombre de nombres déficients entre 100 et 999 est 675. Remarque : il n'existe pas de nombre parfait de trois chiffres.
EXERCICE 3
| > | restart:with(numtheory): |
Warning, the protected name order has been redefined and unprotected
Il s'agit ici de chercher dans l'ensemble {100, 101, 102, ..., 999} le plus grand nombre à trois chiffres dont la somme des diviseurs soit un nombre premier. On peut créer la liste L des nombres de l'ensemble {100, 101, 102, ..., 999} dont la somme des diviseurs est un nombre premier :
| > | L:=NULL: for i from 100 to 999 do if isprime(sigma(i)) then L:=L,i fi; od; L; |
![]()
Ainsi, le plus grand nombre à trois chiffres dont la somme des diviseurs est un nombre premier est 729.
EXERCICE 4
| > | restart: |
| > | x:=t->2*t+1/t;y:=t->t+1+1/(t+1); |
![]()
![]()
x est définie pour t distinct de 0 et y est définie pour t distinct de 1. Il suffit donc de faire des juxtapositions de tracés ne comportant pas les points t=0 et t=-1.
| > | plot({[x(t),y(t),t=-5..-1.1],[x(t),y(t),t=-0.9..-0.1],[x(t),y(t),t=0.1..5]}); |
![[Maple Plot]](partiel2008_mercredi/partiel2008_mercredi36.gif)
Recherche des tangentes verticales d'abord puis horizontales après ...
| > | solve(diff(x(t),t)=0,t); solve(diff(y(t),t)=0,t); |
![]()
![]()
Points où la tangente est verticale ...
| > | simplify([x(1/2*2^(1/2)),y(1/2*2^(1/2))]);simplify([x(-1/2*2^(1/2)),y(-1/2*2^(1/2))]); |
![[2*2^(1/2), (5+2*2^(1/2))/(2^(1/2)+2)]](partiel2008_mercredi/partiel2008_mercredi39.gif)
![[-2*2^(1/2), (-5+2*2^(1/2))/(2^(1/2)-2)]](partiel2008_mercredi/partiel2008_mercredi40.gif)
Point où la tangente est horizontale ...
| > | [x(-2),y(-2)]; |
![]()
Que se passe-t-il en t=0 ?
| > | limit(x(t),t=0,left);limit(x(t),t=0,right);limit(y(t),t=0); |
![]()
![]()
![]()
La droite d'équation y=2 est donc asymptote à la courbe.
Que se passe-t-il en t=-1 ?
| > | limit(x(t),t=-1);limit(y(t),t=-1,left);limit(y(t),t=-1,right); |
![]()
![]()
![]()
La droite d'équation x=-3 est donc asymptote à la courbe.
Que se passe-t-il en
![]() ?
?
| > | limit(x(t),t=infinity);limit(y(t),t=infinity); |
![]()
![]()
Branche infinie, on recherche à préciser le comportement ...
| > | limit(y(t)/x(t),t=infinity);limit(y(t)-x(t)/2,t=infinity); |
![]()
![]()
La droite d'équation y=x/2+1 est donc asymptote à la courbe.
Que se passe-t-il en
![]() ?
?
| > | limit(x(t),t=-infinity);limit(y(t),t=-infinity); |
![]()
![]()
Branche infinie, on recherche à préciser le comportement ...
| > | limit(y(t)/x(t),t=-infinity);limit(y(t)-x(t)/2,t=-infinity); |
![]()
![]()
La droite d'équation y=x/2+1 est donc asymptote à la courbe.
Un nouveau tracé avec les asymptotes ...
| > | plot({[x(t),y(t),t=-5..-1.1],[x(t),y(t),t=-0.9..-0.1],[x(t),y(t),t=0.1..5],[-3,t,t=-10..10],[t,2,t=-10..10],[t,t/2+1,t=-10..10]}); |
![[Maple Plot]](partiel2008_mercredi/partiel2008_mercredi58.gif)
| > | Fin (Philippe RYCKELYNCK & Denis VEKEMANS) |
Error, missing operator or `;`