- Solution
[Créteil, Paris, Versailles, 2004]
1. Quelle est la nature du triangle ACO ?

Dans le cercle de centre O, les 12 triangles AOB, BOC,
COD, DOE, EOF, FOG, GOH, HOI, IOJ,
JOK, KOL et LOA sont isocèles, superposables
(les 3 côtés sont respectivement de même longueur),
les angles
,
,
,
,
,
,
,
,
,
,
et
mesurent donc 360°/12 = 30°.
Dans le triangle ACO, isocèle en O, l'angle
mesure donc 2 x 30° = 60°.
Le triangle ACO est donc isocèle avec un angle au sommet de 60°,
il est donc équilatéral et
la longueur de chaque côté est égal au rayon R
du cercle.
2. Quelle est la nature du polygone ACEGIK ?

ABCDEFGHIJK est un dodécagone régulier : les triangles AOC, COE,
EOG, GOI, IOK et KOA,
sont équilatéraux (la longueur du côté est R - voir question 1.-).
Ainsi, AC = CE = EG = GI = IK = KA = R et ACEGIK
est un hexagone (convexe)
inscrit dans un cercle et dont les côtés sont de même longueur : il est donc
régulier.
3. La droite (AC) coupe la droite (BO) en M.
Que représente la droite (AM) pour le triangle ABO ?
Exprimer AM en fonction du rayon R du cercle circonscrit au dodécagone.

O est équidistant de A et de C ;
de même, B est équidistant de A et de C,
donc la droite (OB) est la médiatrice du segment [AC], puis la droite
(AM) est perpendiculaire à la droite (OB). La droite (AM) représente
donc la hauteur issue de A du triangle AOB.
M est le milieu de [AC] (car M appartient à la médiatrice du
segment [AC]), donc AM = AC/2
= R/2.
4. Exprimer l'aire du triangle ABO en fonction du rayon R du cercle.
En déduire que l'aire d'un dodécagone régulier est donnée par la formule :
Aire = 3 x R2 où R représente
le rayon du cercle circonscrit au dodécagone.

L'aire du dodécagone est donc égale à 12 fois l'aire du triangle AOB.
L'aire du triangle AOB est (AM x OB)/2 =
(R/2 x R)/2 = R2/4.
L'aire du dodécagone est donc 12 x
(R2/4) = 3 x R2.
5. Quelle est l'aire d'un dodécagone régulier inscrit dans un cercle de
diamètre 18 cm ?

Lorsque je prends R = 9 cm, j'obtiens une aire de 3 x
92 cm2 =
3 x 81 cm2 = 243 cm2 pour le dodécagone
régulier.
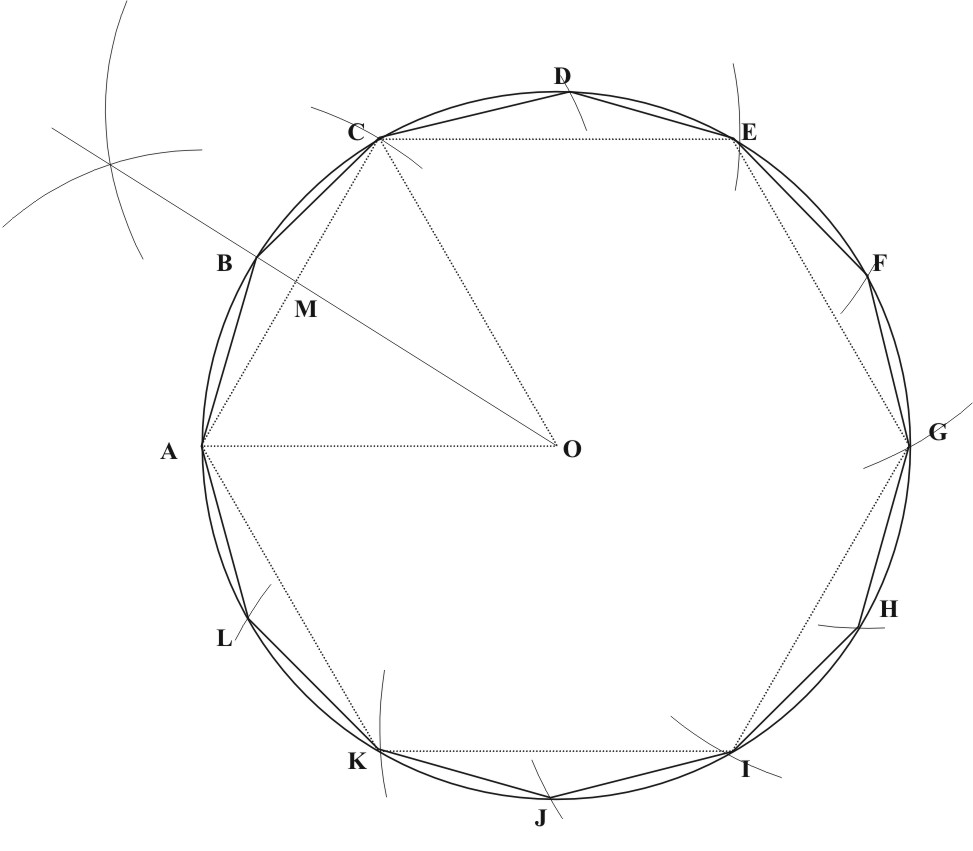
6. Tracer un dodécagone régulier ABCDEFGHIJKL inscrit dans un cercle de
centre O et rayon 6 cm. On utilisera la règle graduée et le compas et
on laissera les traits de construction apparents.