- Solution [Bordeaux, Caen, Clermont, Nantes, Orléans-Tours, Poitiers, La
Réunion, 2000]
1. Prouver que (IL)//(JK) et que IJKL est un
parallélogramme.

Je trace d'abord la figure ...
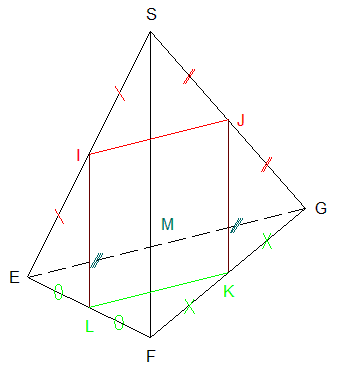
Le théorème de la droite des milieux appliqué dans
le triangle SEG avec I milieu du segment [SE]
et J milieu du segment [SG] donne (IJ)//(EG) et
IJ = EG/2.
Le théorème de la droite des milieux appliqué dans
le triangle FEG avec L milieu du segment [FE]
et K milieu du segment [FG] donne (LK)//(EG) et
LK = EG/2.
Ainsi (IJ)//(EG)//(LK) et les droites (IJ)
et (LK) sont parallèles.
De plus, IJ = EG/2 = LK et IJ = LK.
Le quadrilatère (convexe) IJKL
a ses côtés opposés [IJ] et [LK]
égaux (en mesure) et parallèles, est,
par conséquent un parallélogramme.
2. On suppose, seulement dans cette question, que SF = EG.
Quelle est la nature de IJKL ?

De la même manière que pour la question 1, je sais que (IL)//(SF)//(JK)
et que IL = SF/2 = JK.
Ainsi, si SF = EG, je déduis que IL = SF/2 = EG/2 =
IJ.
Le parallélogramme IJKL possède donc deux
côtés consécutifs [IJ] et [IL]
égaux (en mesure) et IJKL est un
losange.
3. On suppose, seulement dans cette section, que (SF) est
orthogonale au plan (EFG). Démontrer que IJKL
est un rectangle.

Je sais que (SF) ┴ (EFG), mais je sais également que (IL)//(SF).
Je déduis alors que (IL) ┴ (EFG). Puis,
que la droite (IL) est orthogonale à toute droite du
plan (EFG) et en particulier à la droite (LK).
Le parallélogramme IJKL possède donc deux
côtés consécutifs [IL] et [LK]
perpendiculaires et IJKL est un rectangle.
4. Quelle condition suffit-il d'imposer au triangle SEG pour
que le quadrilatère SIMJ soit un losange ?

Le théorème de la droite des milieux appliqué dans
le triangle SEG avec I milieu du segment [SE]
et M milieu du segment [EG] donne (IM)//(SG) et
IM = SG/2. Or J est milieu du
segment [SF], donc SJ = SG/2.
Le quadrilatère (convexe) SIMJ
a ses côtés opposés [IM] et [SJ]
égaux (en mesure) et parallèles, est,
par conséquent un parallélogramme.
Pour que le parallélogramme SIMJ soit un losange, il
suffit qu'il ait deux côtés consécutifs
égaux (en mesure), par exemple SI = SJ (i.e. SE = SF
car SI = SE/2 = SF/2 = SJ).
Sous la condition "le triangle SEF est
isocèle en S", le quadrilatère IJKL est
donc un losange.
5. Quelle condition suffit-il d'imposer au triangle SEG pour
que le quadrilatère SIMJ soit un rectangle ?

Pour que le parallélogramme SIMJ soit un losange, il
suffit qu'il ait deux côtés consécutifs
perpendiculaire, par exemple (SI) ┴ (SJ) (i.e. (SE) ┴ (SF)).
Sous la condition "le triangle SEF est
rectangle en S", le quadrilatère IJKL est donc
un rectangle.
6. Dessiner le patron d'une pyramide SEFG telle que SIMJ
soit un carré et IJKL un rectangle.

Si le triangle SEG est isocèle rectangle en S,
le quadrilatère SIMJ est à la fois losange
(question 4) et rectangle (question 5), donc un carré.
Si (SF) est orthogonale au plan (EFG), alors le
quadrilatère IJKL est un rectangle (question 3).
Ainsi, il s'agit ici de tenir compte de ces deux conditions : - SFE
et SFG sont deux triangles rectangles en F
(ils sont isométriques),
- EFG est un triangle isocèle en F,
- SEG est un triangle isocèle rectangle en S.
Je peux obtenir plusieurs tétraèdres différents.
En effet, le point F peut se déplacer sur le demi-cercle
de diamètre [SE] extérieur au trianggle EGS
(cependant sans trop se rapprocher
du point E)
...
Dans l'animation ci-dessous, le point F1 est mobile.







