- Solution
[Aix,
Marseille, Corse, Montpellier, Nice, Toulouse, 2004]
1) Le point D appartient-il au segment [IG] ? Expliquer.
Les apparences peuvent être trompeuses ...

Le segment [IG] est inclus dans le plan (BCG) et le point D
appartient au plan (ADH). Or, les plans (BCG) et (ADH) sont parallèles
et n'ont par conséquent aucun point en commun ; le point D
n'appartient donc pas au segment [IG].
2) a) Justifier que AC = CH = HF = FA.
Facile !

Les segments [AC], [CH], [HF] et [FA] sont des diagonales de
carrés isométriques. Donc, AC = CH = HF = FA
= 4 x √2 cm.
2) b) Peut-on dire que ACHF est un losange ? Expliquer.
Ce qui est vrai dans le plan ne l'est pas toujours dans l'espace ...

Le segment [CF] est inclus dans le plan (BCG) et le segment [AH]
appartient au plan (ADH). Or, les plans (BCG) et (ADH) sont parallèles
et n'ont, par conséquent, aucun point en commun ; les segments [CF] et [AH]
ne sont donc pas coplanaires, ce qui induit que le quadrilatère
ACHF n'est pas un losange.
3) Démontrer que les quadrilatères AICK, CKJG et AIGJ
sont des parallélogrammes.

Soit O le centre du carré ABCD et sO la symétrie de
centre O.
Je sais que sO(A)=C et que sO(D)=B, donc,
sO([AD])=[CB]
et, la symétrie centrale conservant les milieux, sO(K)=I.
Ensuite, le quadrilatère ICKA admet O comme
centre de symétrie et est donc un
parallélogramme (car un quadrilatère possédant un centre de symétrie
est un parallélogramme).
Je sais que la droite (CG) est orthogonale au plan (BCD), donc
la droite (CG) est orthogonale à toute droite du plan (BCD) et,
en particulier à la droite (CK), ce qui induit que l'angle
est droit.
De même, je sais que la droite (CG) est orthogonale au plan (FGH), donc
la droite (CG) est orthogonale à toute droite du plan (FGH) et,
en particulier à la droite (GJ), ce qui induit que l'angle
est droit.
De plus, les droites (DH) et (KJ) sont parallèles car, comme les droites
(KD) et (JH) sont parallèles, comme KD = JH = 2 cm,
et comme le quadrilatère KDHJ est convexe,
le quadrilatère KDHJ est un parallélogramme.
Puis, comme les droites
(DH) et (CG) sont parallèles, les droites (CG) et (KJ)
sont aussi parallèles (transitivité du parallélisme) (de là, les points C,
G, K et J sont coplanaires).
La droite (KJ) est donc aussi orthogonale au plan (BCD), donc
la droite (KJ) est orthogonale à toute droite du plan (BCD) et,
en particulier à la droite (KC), ce qui induit que l'angle
est droit.
Le quadrilatère CGJK possède donc trois angles
droits et est, par conséquent,
un rectangle (et aussi un parallélogramme).
Les droites (AI) et (KC) sont parallèles et AI = KC car le
quadrilatère AICK est un parallélogramme. D'autre part, les droites (KC) et
(JG) sont parallèles et KC = JG car le
quadrilatère CKGJ est un parallélogramme. Ainsi, comme les droites (AI) et
(JG) sont parallèles (par transitivité du parallélisme) (de là, les points A,
I, G et J sont coplanaires), comme AI = JG (= KC)
et comme le quadrilatère AIGJ est convexe, le quadrilatère
AIGJ est un parallélogramme.
Autre démonstration :
Les triangles AEJ et ILG sont isométriques car ils possèdent deux
mesures de côté et un angle en commun :
AE = IL = 4 cm (car IL = BF puisque, comme les droites
(BI) et (FL) sont parallèles, comme BI = FL = 2 cm,
et comme le quadrilatère BILF est convexe,
le quadrilatère BILF est un parallélogramme) ;
=
= 90° (car le parallélogramme BILF est aussi un rectangle
puisqu'il possède un angle droit en B).
Les triangles AEJ et ILG sont isométriques et sur des faces
parallèles (ADH) et (BCG).
Le polyèdre AEJILG est donc un prisme (oblique) et les faces latérales
AICK, CKJG et AIGJ sont
des parallélogrammes.
4) Démontrer que AIGJ est un losange.
AIGJ est déjà un parallélogramme ...

Le théorème de Pythagore appliqué dans le triangle ABI rectangle en B,
donne AI = √(42 + 22) cm = 2 x √5 cm.
De même, le théorème de Pythagore appliqué dans le triangle AEJ rectangle en E,
donne AJ = √(42 + 22) cm = 2 x √5 cm.
Ainsi, le parallélogramme AIGJ possède deux côtés
consécutifs de même longueur et est, par conséquent,
un losange.
5) Le quadrilatère AIGJ est-il un carré ? Justifier.
Etre ou ne pas être ...

Le segment AG est une diagonale du cube ABCDEFGH, donc
AG = 4 x √3 cm.
En reprenant les résultats quelque peu plus haut,
la droite (KJ) est donc aussi orthogonale au plan (BCD), donc
la droite (KJ) est orthogonale à toute droite du plan (BCD) et,
en particulier à la droite (KI), ce qui induit que l'angle
est droit.
KJ = CG = 4 cm car le quadrilatère CKJG est un rectangle.
AE = KJ = 4 cm puisque, comme les droites
(AK) et (EJ) sont parallèles, comme AK = EJ = 2 cm,
et comme le quadrilatère AKJE est convexe,
le quadrilatère AKJE est un parallélogramme).
Le théorème de Pythagore appliqué dans le triangle IKJ rectangle en K,
donne AI = √(42 + 42) cm = 4 x √2 cm.
Les diagonales du losange AIGJ ne sont donc pas de même longueur et le
losange AIGJ n'est pas un carré.
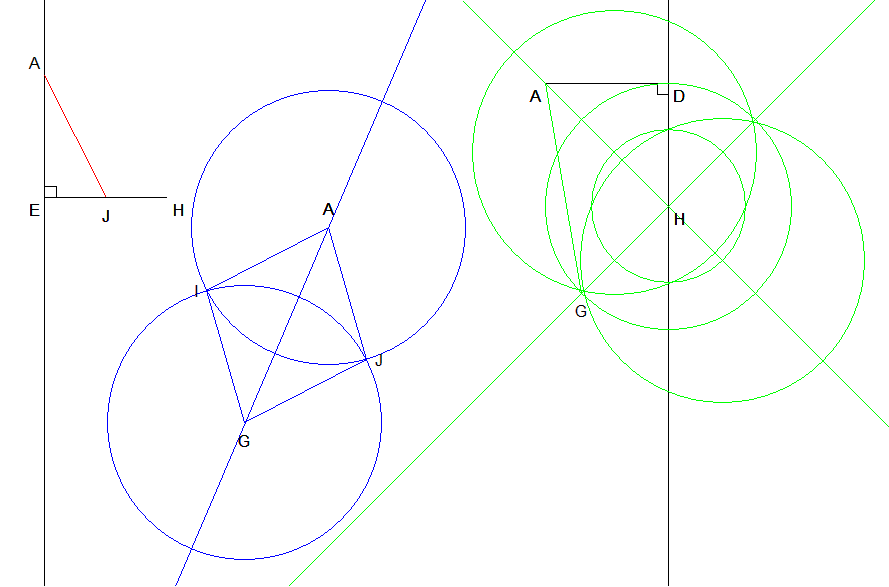
6) Construire, à la règle et au compas, le losange AIGJ en vraie grandeur en
laissant visibles tous les traits de construction. La description de la procédure
de construction n'est pas demandée.

En noir, ce qui est directement repris de la figure.
En rouge, la construction de la longueur AJ.
En vert, la construction du triangle AHG rectangle en H.
En bleu, la construction du losange AIGJ qui utilise le report du
segment [AG], puis le report de la longueur AJ comme rayon de chacun des
deux cercles.