Solution : Aire d'un triangle sur un quadrillage

On ne possède pas de formule directe et le passage par le théorème de Pythagore (pour calculer la longueur de l'un des côtés puis la hauteur relative à ce côté) ou par le théorème de Thalès (quand on découpe le triangle en deux autres en utilisant la trame du quadrillage, pour calculer la longueur des bases de ces nouveaux triangles) serait laborieux.

Je pense donc à décomposer ma figure initiale ...

Et pourquoi pas à l'extérieur du triangle !

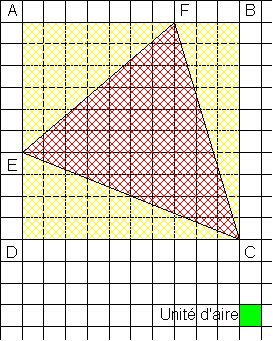
Les sommets ont été nommés pour faciliter l'écriture de la solution ...

On a alors :
Aire(CEF)
= Aire(ABCD) - Aire(AEF) - Aire(BCF) - Aire(CDE)
= 10 x 10 - (6 x 7)/2 - (10 x 3)/2 - (4 x 10)/2
= 100 - 21 - 15 - 20 = 44.