Solution : triangles isocèles

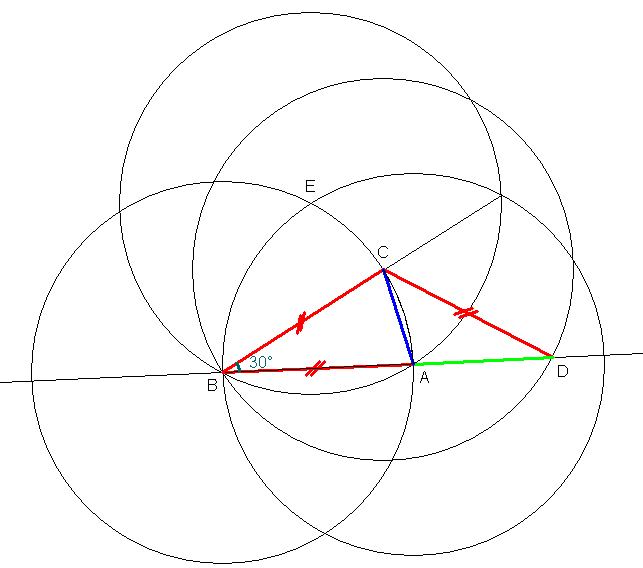
1) Les étapes de la construction, très sommairement :
- construction de ABE équilatéral pour avoir un angle de 60°
- construction de la bissectrice de l'angle en B du triangle ABE pour avoir un angle de 30° et obtenir le point C ;
- construction de BCD isocèle en C.

2) En utilisant dans chacun des trois triangles isocèles l'égalité des angles à la base principale, j'obtiens aisément la figure codée suivante :

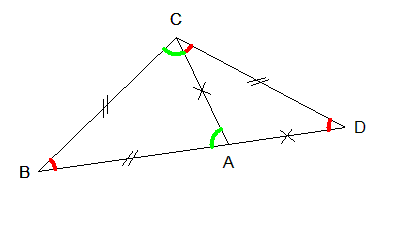
J'appelle x la mesure de l'angle en rouge (i.e. en B dans le triangle ABC, en C ou en D dans le triangle ACD) et y la mesure de l'angle en vert (i.e. en C ou en D dans le triangle ACD).

Deuxc inconnues ... Je cherche alors deux équations ...

On a alors l'angle en A du triangle ACD qui mesure 180° - 2 x x (car la somme des angles d'un triangle mesure 180°).

Aussi, on a l'angle en A du triangle ACD qui mesure 180° - y (car les points B, A et D sont alignés dans cet ordre). De ces deux propriétés, on déduit 2 x x = y.

En utilisant le fait que la somme des angles d'un triangle mesure 180° pour le triangle ABC, on obtient 2 x y + x = 180°. Puis, en utilisant 2 x x = y, on obtient 5 x x = 180°, puis x = 36°.