- Solution
[Besançon, 1998]
1. Calculer DC.

Soit H1 le pied de la hauteur du triangle BCD
issue de D.
Le quadrilatère ABH1D est alors un rectangle
car il possède trois angles droits (en A, en B
et en H1). Par suite, BH1 = AD = 6
cm, DH1 = AB = 6 cm et H1C = BC - BH1
= 12 - 6 cm = 6 cm.
Le théorème de Pythagore utilisé dans
le triangle CH1D, rectangle en H1,
me donne CD = √(CH12
+ DH12) = √(36 + 36) cm =
6 x √2 cm.
2. Calculer la longueur de chacune des arêtes de la pyramide DIJH.

Les six arêtes de la pyramide DIJH sont [DI], [DJ],
[DH], [IJ], [IH] et [JH]. - DI = 2 cm. C'est une
donnée.
- DJ = DC/3 =
2 x √2 cm.
C'est une donnée également.
- J'ai DI/DA = DJ/DC = 1/3 avec D, I et A
alignés dans cet ordre et D, J et C
alignés dans cet ordre. Ainsi, d'après la
réciproque du théorème de Thalès, j'obtiens
(IJ)//(AC) et IJ/AC = 1/3.
Le théorème de Pythagore utilisé dans
le triangle ABC, rectangle en B, me donne AC = √(AB2
+ BC2) = √(36 + 144) cm = 6 x
√5 cm. Puis, IJ = AC/3 = 2 x √5 cm.
- DH = AE = 5
cm. C'est une donnée.
- Le théorème de Pythagore utilisé dans
le triangle IDH, rectangle en D, me donne IH = √(ID2 + DH2) = √(4 +
25) cm = √29 cm.
- Le théorème de Pythagore utilisé dans
le triangle JDH, rectangle en D, me donne JH = √(JD2 + DH2) = √(8 +
25) cm = √33 cm.
3. Construire au compas et à la règle (règle
graduée et non graduée) le triangle IJH en vraie
grandeur en laissant apparents les traits de construction.

Les côtés du triangle IJH mesurent 2 x √5 cm, √29 cm et √33 cm.
Il reste encore à construire ces longueurs ...
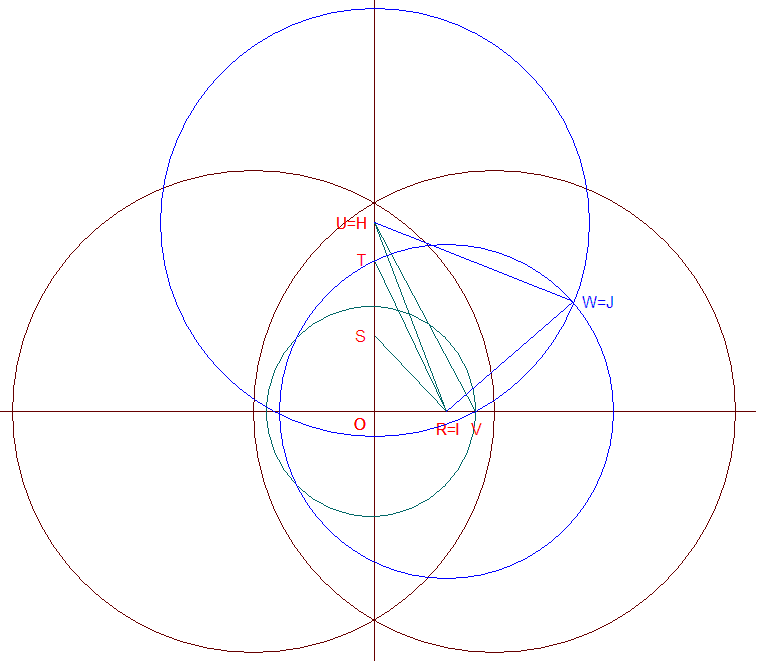
Explications de la construction. - Je construis deux
perpendiculaires d et d' qui se
coupent en un point O.
- Je place R sur la droite d tel que OR = 2
cm.
- Je place S sur la droite d' tel que OS = 2
cm.
- Je place T sur la droite d' tel que OT = 4
cm.
- Je place U sur la droite d' tel que OU = 5
cm.
- Ainsi, RS = 2 x √2 cm, RT = 2
x √5 cm, RU = √29 cm.
- Je trace le cercle de centre O et de rayon 2 x √2 cm qui coupe la droite d en le point
V.
- Ainsi, UV = √33 cm.
- Je trace ensuite le cercle de centre R et de rayon [RT],
et le cercle de centre U et de rayon [UV] qui se
coupent en deux points dont un que je baptise W.
- En posant I = R, H = U et J = W,
j'obtiens le triangle IJH.
4. Calculer l'aire du triangle ACD. En déduire celle du
triangle IJD.

Soit H2 le pied de la hauteur du triangle ACD
issue de C.
Le quadrilatère ABCH2 est est alors un
rectangle car il possède trois angles droits (en A, en B
et en H2). Par suite, CH2 = BA = 6
cm, AH2 = BC = 12 cm.
J'ai Aire(ACD) = (AD x
CH2)/2
= (6 x 6)/2 cm2 = 18 cm2.
Comme ID/AD = JD/CD = IJ/AC = 1/3, je déduis que le
triangle IDJ est une réduction du triangle ADC
de rapport 1/3.
Or, le réduction agit au simple sur les longueurs, au
carré sur les aires et au cube sur les volumes, donc Aire(IDJ) = (1/3)2 x
Aire(ADC) = 2 cm2.
5. Quel est le volume du solide DIJH ?

Volume(DIJH) = (Aire(DIJ) x DH)/3 = 10/3 cm3
([DH] étant une hauteur du prisme, est encore une hauteur
du solide DIJH).






