- Solution
[Corse, 1998]
1. Quelle est la nature du triangle HBC ? Justifier votre
réponse.

Le triangle HBC est rectangle en C car la droite (BC)
est orthogonale
au plan (DCG). En effet, la droite (DC) est
perpendiculaire à la droite (BC) (vu que le
quadrilatère ABCD est un carré) et car la droite (GC)
est perpendiculaire à la droite (BC) (vu que le
quadrilatère BCGF est un carré).
Ainsi, la droite (BC) est perpendiculaire à toute droite
du plan (DCG) et en particulier à la droite (CH).
2. On étudie le triangle HDB. - 2.a) Calculer les
mesures exactes DB et HB. (Tous
les calculs doivent être justifiés.)
- 2.b) Démontrer que les droites (KI) et (HB)
sont parallèles. En déduire KI.
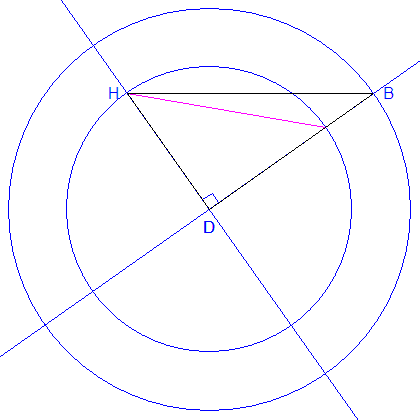
- 2.c) Dessiner le triangle HDB en vraie grandeur.

De la même façon que pour la première question, je
montrerais que le triangle HDB est rectangle en D.
[DB] est une diagonale du carré ABCD. Une
application directe du théorème
de Pythagore me fournit que DB = 6 x √2 cm.
Dans le triangle HDB rectangle en D, le
théorème de Pythagore me donne HB
= √(HD2 + DB2) = 6 x √3 cm.
Dans le triangle HDB, I est milieu du segment [DB]
et K est milieu du segment [DH]. Le
théorème de la droite des milieux me permet de
déduire
que les droites (IK) et (BH)
sont parallèles.
De plus, j'aurai KI = HB/2 = 6 x √3 cm.
La question portant sur le dessin du triangle HDB ne requiert,
a priori, pas de construction.
Il me suffit donc de fournir un dessin sans explication ...
3. On considère la pyramide de sommet H ayant pour base
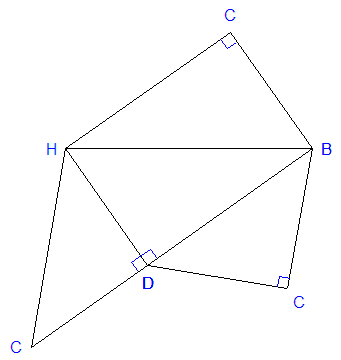
le triangle BCD. - 3.a) En dessiner un patron à
l'échelle 1:2.
- 3.b) Calculer le volume de cette pyramide.

Là encore, il me suffit de fournir un dessin sans explication
...
Et le volume de cette pyramide ...
Volume(BCDH) = (Aire(BCD) x DH)/3 = (BC x CD x DH)/6 = 36 cm3 ([HD] étant une
hauteur du cube, est encore une hauteur de
la pyramide BCDH).





