Sujet de Grenoble, 1998.
Réponses
Séance 16.
L'analyse porte sur l'exercice 1 de la rubrique Exercices et Problèmes,
en bas de l'annexe A.
a) Décrire brièvement les procédures attendues pour reproduire les figures B, C et D
sur du papier quadrillé identique à celui du manuel (en précisant, pour chacune des
procédures, les instruments utilisés et les notions mathématiques sous-jacentes).
Sur papier quadrillé, on ne peut attendre qu'une procédure liée au repérage des sommets des
différents quadrilatères ...
- - soit par un tracé consécutif, en suivant les côtés, ce qui donnerait pour la figure B,
par exemple, "Je place le premier
sommet sur un noeud du quadrillage ; pour placer le deuxième sommet, je me déplace de
trois carreaux vers la droite, et de trois carreaux vers le haut ; pour placer le troisième
sommet, je me déplace ensuite de trois carreaux vers la droite et de trois carreaux vers le bas ;
et pour placer le dernier sommet, je me déplace ensuite de trois carreaux vers la gauche et de trois
carreaux vers le bas" ;
- - soit par un tracé à partir d'un sommet fixe, en utilisant également les diagonales,
ce qui pourrait donner pour la figure B, par exemple, "Je place le premier
sommet sur un noeud du quadrillage ; pour placer le deuxième sommet, je me déplace de
trois carreaux vers la droite, et de trois carreaux vers le haut ; pour placer le troisième
sommet, je me déplace depuis mon premier sommet de six carreaux vers la droite ;
et pour placer le dernier sommet, je me déplace depuis mon premier sommet de trois
carreaux vers la droite et de trois carreaux vers le bas" ;
- - ...
Matériel : une règle non graduée suffit.
b) Décrire brièvement les procédures attendues pour reproduire les figures B, C et D
sur du papier uni (en précisant, pour chacune des
procédures, les instruments utilisés et les notions mathématiques sous-jacentes).
La question porte sur la reproduction de figures et présuppose que l'élève est
capable de reconnaître les différents quadrilatères (B : un carré ; C : un rectangle et
D : un losange). Cependant, il est probable que les
propriétés (concernant les côtés, les diagonales, ...) qui permettent de reconnaître tel
ou tel quadrilatère influent sur la reproduction de la figure ...
Procédures pour la reproduction du carré B ...
- - utilisant les diagonales (plus probable que par les côtés car les diagonales sont portées
par la trame du quadrillage et l'orthogonalité des diagonales est plus facile à repérer que celles
des diagonales) : les diagonales sont de même longueur, perpendiculaires et se coupent en
leur milieu ;
- - utilisant les côtés : les côtés sont de même longueur et perpendiculaires quand
consécutifs.
Matériel : la règle graduée (pour tracer des droites et reporter des longueurs) et
l'équerre (pour reporter des angles droits) ... il est peu probable que le compas soit
utilisé, tant pour reporter des longueurs que pour reporter des angles droits.
Procédures pour la reproduction du rectangle C ...
- - utilisant les côtés (beaucoup plus probable que par les diagonales car les côtés
sont tracés et portés
par la trame du quadrillage et l'orthogonalité des côtés est alors facile à repérer) :
les côtés sont perpendiculaires quand consécutifs ;
- - utilisant les diagonales (difficile) : les diagonales sont de même longueur et
se coupent en leur milieu ... mais pour cette reproduction, il faut aussi pouvoir reporter
l'angle formé par les diagonales.
Matériel : la règle graduée (pour tracer des droites et reporter des longueurs) et
l'équerre (pour reporter des angles droits) et, si nécessaire, le gabarit d'angle (pour reporter
un angle non droit) ... il est peu probable que le compas soit
utilisé, tant pour reporter des longueurs que pour reporter des angles (droits ou non) ; de même,
il est probable que les élèves préféreront le gabarit d'angle au rapporteur dont l'utilisation
pose souvent de sérieux problèmes.
Procédures pour la reproduction du losange D ...
- - utilisant les côtés (difficile, mais plus probable que par les diagonales car si les côtés sont
tracés, ce n'est pas le cas des diagonales ... même s'il est usuellement plus facile de construire
un losange à partir de ses diagonales) :
les côtés sont de même longueur ... mais pour cette reproduction, il faut aussi pouvoir reporter
l'angle formé par deux côtés consécutifs ;
- - utilisant les diagonales (relativement plus facile que la procédure proposée ci-dessus) :
les diagonales sont perpendiculaires et
se coupent en leur milieu.
Matériel : la règle graduée (pour tracer des droites et reporter des longueurs) et,
si nécessaire, le gabarit d'angle (pour reporter
un angle non droit) et, si nécessaire, l'équerre (pour reporter des angles droits) ...
il est peu probable que le compas soit
utilisé, tant pour reporter des longueurs que pour reporter des angles (droits ou non) ;
de même, il est probable que les élèves préféreront le gabarit d'angle au
rapporteur dont l'utilisation
pose souvent de sérieux problèmes.
c) Hiérarchiser les figures B, C et D selon la difficulté de leur production,
en justifiant la réponse.
Par ordre croissant de difficulté : C, B et D ou B, C et D.
- Au niveau de la reproduction (bien sûr, au niveau de la reconnaissance des figures, il est plus aisé
de traiter le rectangle C que le carré B qui n'est pas dans son orientation usuelle),
les figures B et C proposent exactement la même
difficulté lorsque le tracé s'effectue côté par côté.
- La reproduction de la figure D est, quant à elle, plus complexe.
d) En déduire les rôles que l'on peut attribuer à chacune de ces deux activités
et à leur enchaînement au regard des objectifs mentionnés sous le titre du chapitre 16.
La phase sur papier quadrillé permet de visualiser et s'approprier (à l'aide du repérage
des sommets) quelques propriétés des différents
quadrilatères proposés (certaines mesures des côtés ou des diagonales, perpendicularité),
et la seconde phase sur papier uni propose ensuite d'utiliser ces propriétés dans
une construction outillée.
L'articulation des deux phases sert donc intégralement l'objectif de la séance :
"Identifier le losange, le rectangle, le carré par certaines de leurs propriétés. Utiliser
ces propriétés pour les construire".
e) Quelle(s) contrainte(s) non recherchée(s) risque(nt) d'être introduite(s)
dans la reproduction, qui ne concerne(nt) pas les objectifs définis.
Les figures ont des positions relatives qui ne doivent probablement pas être reproduites,
mais qui risquent de l'être.
Les lettres nominative des quadrilatères semblent imposer une certaine chronologie du tracé
des différentes figures, ce qui n'est probablement pas souhaité.
Séance 28.
L'analyse porte sur la rubrique Découverte de l'annexe B et sur l'extrait du
livre du maître correspondant de l'annexe C.
a) Quels choix faits aux points I, II, et III du livre du maître (annexe C) expliquent
la difficulté que peuvent avoir des élèves pour reproduire la rosace à huit pétales ?
- Quelle est la raison d'être de ces choix ?
Le livre du maître souligne que les enfants peuvent confondre la rosace à huit branches
avec la plus familière rosace à six branches.
Un autre point à souligner est la difficulté pour les élèves de reproduire une rosace
présentée uniquement au tableau : les élèves sont dans l'incapacité de manipuler
la figure (par exemple, pour chercher les positions des centres des différents
arcs de cercles) et doivent se contenter d'une simple intuition visuelle.
L'objectif annoncé de la séance est : "Analyser une figure géométrique, faire des
hypothèses de construction, les vérifier, utiliser les instruments de géométrie".
Les choix précédents pourraient donc avoir pour but de faire comprendre aux élèves
que la manipulation outillée est indispensable pour analyser une figure (le livre du maître
prévoit d'ailleurs "un blocage").
b) Donner deux stratégies de construction, avec règle et compas seulement sur feuille
blanche, induites respectivement par les figures B et C de l'annexe C.
- On laissera apparents les traits de construction.
- Chacune des deux stratégies sera décrite par une suite d'instructions.
Figure B
Je trace une droite d, je place O un point sur la droite d
et je trace un cercle Γ de centre O. La droite d et le cercle
Γ se coupent en les points C et G distincts.
Je trace deux cercles, de centres respectifs C et G, de même rayon (suffisamment grand)
qui se coupent en deux points qui définissent la médiatrice d' du segment [CG]
et qui est, conséquemment, perpendiculaire à la droite d. La droite d' et le cercle
Γ se coupent en les points A et E distincts.
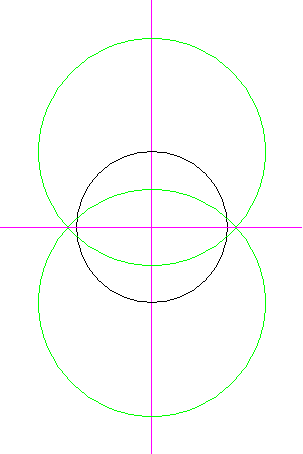
Je trace trois cercles, de centres respectifs A, C et E, de même rayon (suffisamment grand).
Les deux premiers se coupent en deux points qui définissent la médiatrice
δ du segment [AC] et les deux derniers se coupent en deux points qui définissent la médiatrice
δ' du segment [CE].
La droite δ et le cercle
Γ se coupent en les points B et F distincts (B est choisi
de façon à ce que le quadrilatère OABC soit convexe).
La droite δ' et le cercle
Γ se coupent en les points D et H distincts (D est choisi
de façon à ce que le quadrilatère OCDE soit convexe).
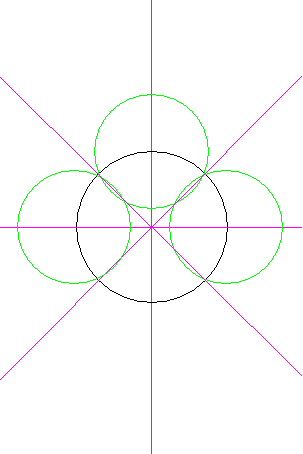
Je trace les carrés ACEG et BDFH.
Les droites (AC) et δ se coupent en B',
milieu du segment [AC].
Les droites (CE) et δ' se coupent en D',
milieu du segment [CE].
Les droites (EG) et δ se coupent en F',
milieu du segment [EG].
Les droites (GA) et δ' se coupent en H',
milieu du segment [GA].
Les droites (BD) et d se coupent en C',
milieu du segment [BD].
Les droites (DF) et d' se coupent en E',
milieu du segment [DF].
Les droites (FH) et d se coupent en G',
milieu du segment [FH].
Les droites (HB) et d' se coupent en A',
milieu du segment [HB].
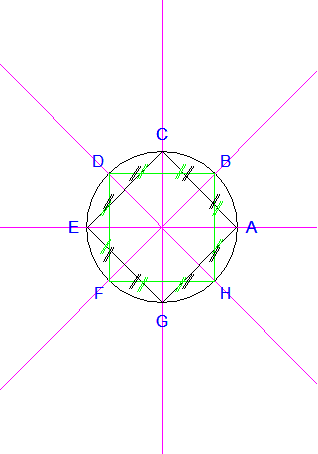
Je trace les cercles de centres respectifs A', B', C', D', E',
F', G', et H', passant tous par O.
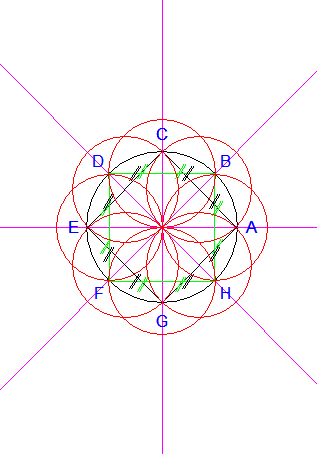
Figure C
Je trace une droite d, je place O un point sur la droite d
et je trace un cercle Γ de centre O. La droite d et le cercle
Γ se coupent en les points C et G distincts.
Je trace deux cercles, de centres respectifs C et G, de même rayon (suffisamment grand)
qui se coupent en deux points qui définissent la médiatrice d' du segment [CG]
et qui est, conséquemment, perpendiculaire à la droite d. La droite d' et le cercle
Γ se coupent en les points A et E distincts.

Je trace trois cercles, de centres respectifs A, C et E, de même rayon (suffisamment grand).
Les deux premiers se coupent en deux points qui définissent la médiatrice
δ du segment [AC] et les deux derniers se coupent en deux points qui définissent la médiatrice
δ' du segment [CE].
La droite δ et le cercle
Γ se coupent en les points B et F distincts (B est choisi
de façon à ce que le quadrilatère OABC soit convexe).
La droite δ' et le cercle
Γ se coupent en les points D et H distincts (D est choisi
de façon à ce que le quadrilatère OCDE soit convexe).

Je trace les cercles de centres respectifs A, B, C, D, E,
F, G, et H, passant tous par O.
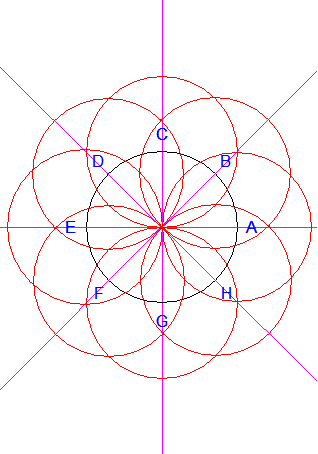
c) Pour chacune des stratégies décrites en b), en quoi le papier quadrillé est-il facilitateur
pour les élèves ?
En faisant coïncider le point O avec un noeud du quadrillage, le tracé des
droites d, d', δ et δ' est facilité :
les droites d et d' pouvant être portées par la trame du quadrillage, auquel cas les
droites δ et δ' ont des directions privilégiées.







