- Solution [Lyon, 1998]
Je commence par tracer le solide BDJIB'D'J'I' en perspective
cavalière.

1. Construire le quadrilatère BDJI à la
règle non graduée et au compas. Indiquer sa nature.
Calculer son aire en fonction de a.

Dans l'ordre et en bref l'explication de la construction de la figure
... - a) construction du segment [AB] de longueur a ;
- b) construction du milieu I du segment [AB]
(construction de la médiatrice (M1M2)
du segment [AB]) ;
- c) construction de la perpendiculaire à la droite (AB)
passant par A (construction du symétrique I' de I
par rapport au point A, puis construction de la
médiatrice (N1N2) du segment [II'])
;
- d) construction du point D ;
- e) construction du milieu J du segment [AD]
(construction de la médiatrice (N1N2)
du segment [AD]) ;
- f) construction du point O, centre du carré (comme
intersection des médianes [M1M2]
et [N1N2]) ;
- g) construction du symétrique C de A par
rapport au point O.
- Les étapes f) et g) sont inutiles pour l'obtention du
quadrilatère BDJI.
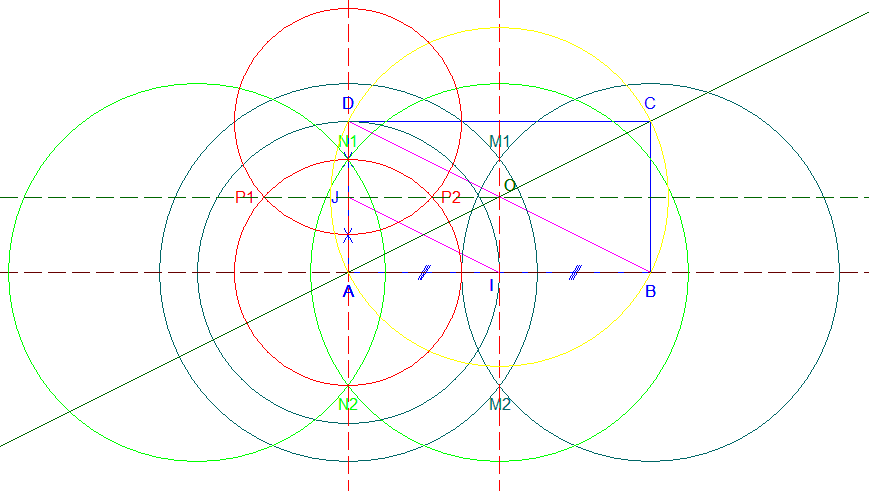
Pour montrer que le quadrilatère BDJI
est un trapèze, il suffit d'utiliser le
théorème de la droite des milieux dans le triangle ABD
où I est milieu du segment [AB] et où J
est milieu du segment [AD] pour obtenir (IJ)//(BD).
Calcul de l'aire du trapèze BDJI : Aire(BDJI) = Aire(BAD) - Aire(IAJ) = (AB x AD)/2 - (AI x AJ)/2 = (3 x a2)/16.
2. Proposer un patron du solide S.
 .
.
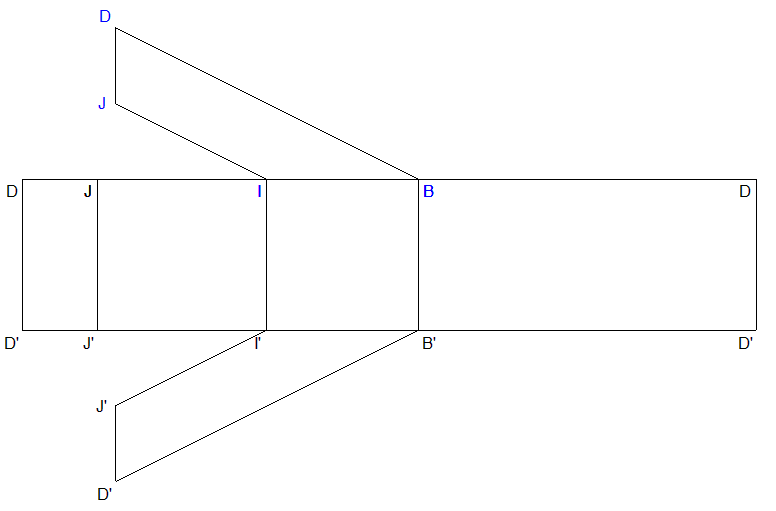
3. Quelle est l'aire totale de ce solide exprimée en fonction de
a ?
Il s'agit donc de l'aire du patron proposé.

Aire totale = Aire(IBB'I') + Aire(BDD'B') + Aire(DJJ'D') +
Aire(JII'J') + Aire(BDJI) + Aire(B'D'J'I').
Le théorème de Pythagore appliqué au triangle ABD
rectangle en B, donne BD = a x √5/2.
Le théorème de la droite des milieux dans le triangle ABD
où I est milieu du segment [AB] et où J
est milieu du segment [AD] donne IJ = BD/2 = a x √5/4.
Retour sur la calcul d'aire (avec toutes les conditions admises sur
certaines faces, il s'agit bien d'un prisme droit) : Aire totale = a/2 x a/4
+ a/2 x a x √5/2 +
a/2 x a/2 +
a/2 x a x √5/4 +
2 x (3 x a2/16)
= a2/8 x (6
+ 3 x √5).
4. Quelle proportion du volume du parallélÚpipède initial
représente le volume de ce solide S ?

Volume(BDJIB'D'J'I') = Aire(BDJI) x BB' =
(3 x a2/16) x
a/2
= 3 x a3/32.
Volume(ABCDA'B'C'D') = Aire(ABCD) x BB' =
AB x AC x BB' = a3/4.
Le rapport des volumes se calcule aisément : Volume(BDJIB'D'J'I')/Volume(ABCDA'B'C'D')
= (3 x a3/32)/(a3/4) = 3/8.







