Sujet d'Aix, Marseille, Montpellier, Nice, 1999.
    Attention : dans les documents proposés, quelquefois l'objectif est de faire travailler l'élève en utilisant le coefficient de proportionnalité, mais ceci est en dehors des programmes de 2002 (et le sujet date d'avant 2002).
    Réponses
    Etude de l'extrait n°1 : (annexe 1).
    1) Quelles sont les compétences mathématiques nécessaires pour répondre aux questions des exercices 1 et 2 ?
    Pour l'exercice 1 :
    Pour l'exercice 2 :
    2) Paragraphe "J'ai appris".
    Dans ce paragraphe, l'auteur propose une définition de proportionnalité et une méthode de résolution.
    Sur quelles propriétés mathématiques de la proportionnalité s'appuient-elles ?
    La définition de la proportionnalité de ce paragraphe s'appuie sur le fait que le prix unitaire peut être utilisé comme coefficient de proportionnalité (si un objet coûte x euros, n objets coûtent alors n x x euros).
    La méthode de résolution proposée s'appuie sur la propriété additive de la fonction linéaire (voir question 1).
    3) Exercices 3 et 4.
    Pour chaque situation proposée, par quelle(s) procédure(s) un élève peut-il répondre à la question posée ?
    En quoi le choix des nombres induit-il cette (ces) procédure(s) ?
    I) Sucettes ...
    Remarque : Il faut lire "Un lot de 7 sucettes ..." au lieu de "Un lot de 7 paquets de ces mêmes sucettes ...".
    Première procédure possible :
    A. Calcul du prix unitaire parmi les 3 sucettes
    B. Calcul du prix unitaire parmi les 7 sucettes
    C. Comparaison des prix unitaire des sucettes dans chacun des deux lots.
    Deuxième procédure possible :
    A. Calcul du prix unitaire parmi les 3 sucettes
    B. Calcul du prix de 7 sucettes à l'aide du prix unitaire des 3 sucettes (calcul multiplicatif).
    C. Comparaison des prix de 7 sucettes.
    Troisième procédure possible :
    A. Calcul du prix unitaire parmi les 7 sucettes
    B. Calcul du prix de 3 sucettes à l'aide du prix unitaire des 7 sucettes (calcul multiplicatif).
    C. Comparaison des prix de 3 sucettes.
    NB : au lieu du calcul du prix unitaire ... variante pour le calcul du prix de 21 sucettes (où 21 = PPCM(3,7)) ; ...
    Le choix des nombres ne permet pas de décider parmi la première, la deuxième ou la troisième, quelle est la plus simple. Par contre, ce choix des nombres rend plus probable les a) que les b) vu que les produits 3 x 9 = 27 et 7 x 9 = 63 sont mémorisés dans les tables de multiplication.
    Résumé (première procédure) ...
    II) Places à l'opéra ...
    Première procédure possible :
    A. Calcul du prix unitaire parmi les 6 places
    B. Calcul du prix unitaire parmi les 15 places
    C. Comparaison des prix unitaire des places dans chacun des deux lots.
    Deuxième procédure possible :
    A. Calcul du prix unitaire parmi les 6 places
    B. Calcul du prix de 15 places à l'aide du prix unitaire des 6 places (calcul multiplicatif).
    C. Comparaison des prix de 15 places.
    Troisième procédure possible :
    A. Calcul du prix unitaire parmi les 15 places
    B. Calcul du prix de 6 places à l'aide du prix unitaire des 15 places (calcul multiplicatif).
    C. Comparaison des prix de 6 places.
    NB : au lieu du calcul du prix unitaire ... variante pour le calcul du prix de 3 places (où 3 = PGCD(6,15)) ; variante pour le calcul du prix de 30 places (où 30 = PPCM(6,15)) ; ...
    En CM1, les élèves ont déjà l'habitude d'utiliser la division et la sous-procédure b) sera probablement plus fréquente que la a). D'autre part, la deuxième et la troisième procédure présentent l'avantage de ne nécessiter qu'une seule division (ou tâtonnement dans la multiplication à trou). Elles sont en plus facilitées par le fait que le diviseur est petit et que le quotient est entier.
    De plus, les variantes utilisant le calcul du prix de 3 places (dans la deuxième procédure) ou de 30 places (toujours dans la deuxième procédure) ne nécessitent qu'un division par 2, ce qui est faisable, même de tête, par les élèves. Autrement, les variantes utilisant le calcul du prix de 3 places (dans la troisième procédure) ou de 30 places (toujours dans la troisième procédure) ne nécessitent qu'un division par 5, ce qui est faisable, même de tête, par les élèves (on multiplie par 2 et on divise par 10).
    Résumé (deuxième procédure, variante utilisant le calcul du prix de 3 places) ...
    III) Classeurs ...
    Première procédure possible :
    A. Calcul du prix unitaire parmi les 4 classeurs
    B. Calcul du prix unitaire parmi les 10 classeurs (utilisation de la règle des zéros).
    C. Comparaison des prix unitaire des classeurs dans chacun des deux lots.
    Deuxième procédure possible :
    A. Calcul du prix unitaire parmi les 4 classeurs
    B. Calcul du prix de 10 classeurs à l'aide du prix unitaire des 4 classeurs (calcul multiplicatif).
    C. Comparaison des prix de 10 classeurs.
    Troisième procédure possible :
    A. Calcul du prix unitaire parmi les 10 classeurs (utilisation de la règle des zéros).
    B. Calcul du prix de 4 classeurs à l'aide du prix unitaire des 10 classeurs (calcul multiplicatif).
    C. Comparaison des prix de 4 classeurs.
    NB : au lieu du calcul du prix unitaire ... variante pour le calcul du prix de 2 places (où 2 = PGCD(4,10)) ; variante pour le calcul du prix de 20 places (où 20 = PPCM(4,10)) ; ...
    En CM1, les élèves ont déjà l'habitude d'utiliser la division et la sous-procédure b) sera probablement plus fréquente que la a) (l'élève ira-t-il chercher les quarts d'euros par tâtonnement ?). D'autre part, la deuxième et la troisième procédure présentent l'avantage de ne nécessiter qu'une seule division (ou tâtonnement dans la multiplication à trou). La troisième procédure est encore facilitée par le fait que le diviseur est 10 et que le quotient est entier.
    Les variantes utilisant le calcul du prix de 2 places (dans la deuxième procédure) ou de 20 places (toujours dans la deuxième procédure) ne nécessitent qu'un division par 2, ce qui est faisable, même de tête, par les élèves.
    Résumé (troisième procédure) ...
    IV) Blousons ...
    Première procédure possible :
    A. Calcul du prix d'1 blouson
    B. Calcul du prix de 14 blousons (calcul multiplicatif).
    Deuxième procédure possible :
    Utilisation de la propriété multiplicative de linéarité (calcul multiplicatif).
    Le choix des nombres est tel qu'il rend difficile la première procédure (division par 7) et très simple la deuxième (multiplication par 2).
    Résumé (deuxième procédure) ...
    V) Manteaux ...
    Procédure possible :
    A. Calcul du prix d'1 manteau
    B. Calcul du prix de 13 manteaux (calcul multiplicatif).
    En CM1, les élèves ont déjà l'habitude d'utiliser la division et la sous-procédure b) sera probablement plus fréquente que la a).
    Le choix des nombres est tel qu'il rend difficile toute autre procédure (une utilisation des propriétés de linéarité est semble-t-il évitée).
    Résumé ...
    Etude de l'extrait n°2 : (annexe 2).
    4) Exercices 1 et 2 de "Je découvre" et "Je m'entraîne".
    Par rapport à la notion en jeu et les problèmes proposés, quels sont les avantages et les inconvénients des tableaux donnés ou à construire ?
    Avantages
    Inconvénients
    5) En tenant compte de tous les éléments qui servent à la présentation de l'exercice 3 ...
    Montrer que l'on peut obtenir des graphiques différents. Est-ce, d'après vous, l'intention de l'auteur ?
    Si on ne porte que les points correspondant à un nombre de boîtes achetées qui est un multiple de 3 (comme c'est suggéré dans le tableau de valeurs et dans le graphique), on obtient un graphique de points alignés et qui semble être propre à une situation de proportionnalité.
    Par contre, si on porte tous les points correspondant à un nombre entier de boîtes achetées, on obtient un graphique de points non alignés et qui montre que la situation ne relève pas de la proportionnalité.
    Ce n'est probablement pas l'intention de l'auteur qui montre à deux reprises qu'il ne compte s'intéresser qu'aux points correspondant à un achat d'un nombre de boîtes qui soit une multiple de 3. De surcroît, l'auteur a intitulé ses pages "la proportionnalité" : il va donc vouloir exhiber que dans une situation de proportionnalité, les points sont alignés sur une droite passant par l'origine.
    Etude comparative des deux extraits.
    6) Comparer ces deux extraits de manuels en ce qui concerne les objectifs poursuivis par les auteurs, les méthodes de résolutions proposées, l'initiative laissée à l'élève.
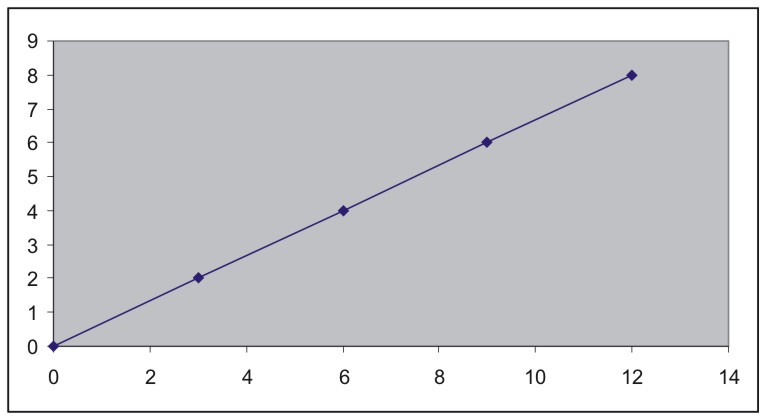
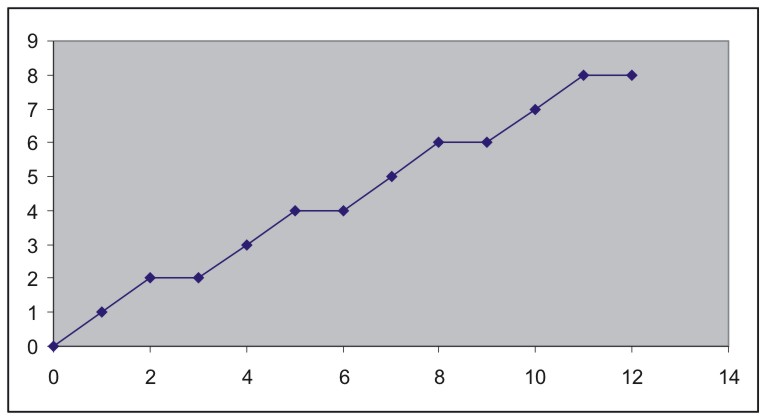
Extrait n°1 Extrait n°2
Objectifs
A) Apprendre à reconnaître des situations relevant ou non de la proportionnalité (les deux types de situations sont proposées).
B) Apprendre à résoudre des problèmes de proportionnalité (dans un contexte de tarifs) en utilisant tantôt le coefficient de proportionnalité (ici le tarif à l'unité), tantôt les propriétés de linéarité (l'élève peut choisir parmi l'une ou l'autre méthode).
C) Lier les supports (problèmes littéraux, tableaux de proportionnalité, graphique) n'est pas obligatoire (l'élève peut choisir parmi les différents supports celui qui lui convient le mieux pour résoudre la situation).
A) L'accent n'est pas mis sur la reconnaissance d'une situation de proportionnalité (toutes les situations présentées sont de proportionnalité).
B) Apprendre à résoudre des problèmes de proportionnalité en utilisant le coefficient de proportionnalité.
C) Voir la proportionnalité en rattachant plusieurs supports (problèmes littéraux, tableaux de proportionnalité, graphique).
Méthodes de résolution
Utilisation tantôt du coefficient de proportionnalité (ici le tarif à l'unité), tantôt des propriétés de linéarité (l'élève choisit selon les nombres proposés).
Utilisation du coefficient de proportionnalité (dans des tableaux de proportionnalité).
Initiative laissée à l'élève L'élève a le choix de la procédure de résolution. Le travail de l'élève est fortement guidé (très peu d'initiative est laissée à l'élève). Les tableaux de proportionnalité apparaissent comme un deuxième problème et non pas comme un outil de résolution. Le graphique n'apparaît pas non plus comme un outil de résolution.