Solution [Amiens, 1999]

Tracer en utilisant une règle graduée et un compas, un triangle ABC rectangle en A tel que AB = 4 cm et BC = 8 cm.

Je me propose de donner un algorithme de construction et de le justifier.

Je trace un segment [OB] de 4 cm. Je trace le cercle C₁ de centre O et de rayon OB et le cercle C₂ de centre B et de rayon BO. Je trace la droite (OB). La droite (OB) coupe le cercle C₁ en deux points distinct B et C. Les cercles C₁ et C₂ se coupent en deux points dont l'un que je nomme A.

Voici la figure ...

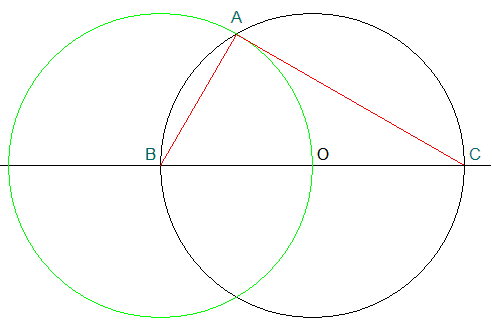
J'ai bien AB = 4 cm (car A appartient au cercle C₂) ; j'ai bien également BC = 8 cm (car [BC] est un diamètre du cercle C₁ puisque B et C appartiennent à C₁ et [BC] contient le centre du cercle C₁) ; et j'ai aussi le fait que le triangle ABC est rectangle en A (car A appartient au cercle de diamètre [BC]).

On considère O le milieu de [BC].
1.a) Comparer OA et BC.
1.b) Calculer l'aire exacte du triangle ABC.
1.c) Donner une valeur approchée de cette aire à 0,1 cm² près (1,732 est une valeur approchée de √3 à 0,001 près).

Je peux commencer par remarquer que le triangle OAB est équilatéral ...

Le triangle OAB est équilatéral (en effet, OB = 4 cm -voir construction- ; OA = 4 cm car A appartient au cercle C1 ; AB = 4 cm -c'est déjà vu-). Ainsi, 0A = BC/2.

Ensuite, la hauteur h du triangle OAB est 4 x √3/2 cm = 2 x √3 cm (voir application directe du théorème de Pythagore). Enfin, l'aire du triangle ABC est Aire(ABC) = (h x BC)/2 = (2 x √3 x 8)/2 cm² = 8 x √3 cm².

L'énoncé me dit que 1,732 est une valeur approchée de √3 à 0,001 près, je déduis donc que 1,731 ≤ √3 ≤ 1,733. Par conséquent, 1,731 x 8 cm² ≤ Aire(ABC) ≤ 1,733 x 8 cm², puis 13,848 cm² ≤ Aire(ABC) ≤ 13,864 cm², et enfin, Aire(ABC) = 13,8 cm² à 0,1 cm² près, par défaut.

Placer E tel que C soit milieu de [AE].
2.a) Quelle est la nature du triangle ABE ?
2.b) Déterminer le rapport des aires des triangles ABE et ABC.
2.c) Déterminer l'aire exacte du triangle BCE.

Je complète d'abord la figure ...

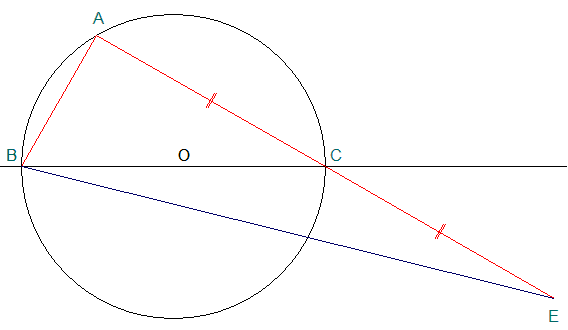
La droite (AC) est perpendiculaire à la droite (AB) car le triangle ABC est rectangle en A. Or, les droites (AC) et (AE) sont confondues, donc les droites (AE) et (AB) sont perpendiculaires et le triangle ABE est rectangle en A.

J'obtiens alors Aire(ABC) = (AB x AC)/2 et Aire(ABE) = (AB x AE)/2, et, par conséquent, Aire(ABE)/Aire(ABC) = AE/AC = 2 (car C est milieu du segment [AE]).

On considère H le point d'intersection du cercle de centre O et de diamètre [BC], avec la droite (BE).
3.a) Démontrer que (CH) est une hauteur du triangle BCE.

Je poursuis l'avancement de la figure.

H appartient au cercle C₁ et [BC] est un diamètre du cercle C₁, donc le triangle HCB est rectangle en H. La droite (CH) est donc perpendiculaire à la droite (BE) et est la hauteur du triangle BCE issue de C.

Placer F tel que C soit milieu de [BF].
3.b) Quelle est la nature du quadrilatère AFEB ?
3.c) Quelle est son aire exacte ?
3.d) Exprimer l'aire d'un losange en fonction de la mesure des diagonales.
3.e) Construire un losange MPNQ à partir de ses diagonales qui ait la même aire que AFEB. Pour cela, vous utiliserez uniquement le compas (qui vous permettra de reporter les longueurs de la première figure) et une règle non graduée.

J'achève la figure.

Le quadrilatère AFEB a ses diagonales qui se coupent en leur milieu C (C est milieu du segment [AE] et du segment [BF]). Le quadrilatère AFEB est donc un parallélogramme.

Aire(AFEB) = AB x AE (car le quadrilatère AFEB est un parallélogramme et car la droite (AE) est perpendiculaire à la droite (AB)). Puis Aire(AFEB) = 2 x AB x AC = 4 x Aire(ABC) = 32 x √3 cm².

Soient d₁ et d₂ les longueurs des deux diagonales d'un losange, alors, l'aire de ce losange est donnée par (d₁ x d₂)/2 (c'est du cours !).

Pour construire un losange MPNQ de même aire que le parallélogramme AFEB, je pose B = M et C = P, puis je construis le point N tel que A soit milieu du segment [MN] et enfin Q tel que A soit milieu du segment [PQ] (les diagonales [MN] et [PQ] se coupent donc en leur milieu A et sont perpendiculaires -car le triangle ABC est rectangle en A-, ce qui induit que MPNQ est un losange ; de plus, ce losange MPNQ a une aire donnée par Aire(MPNQ) = 4 x Aire(ABC) et est donc égale à celle du parallélogramme AFEB).

La construction du losange ...