- Solution [Bordeaux,
Clermont, Nantes, Poitiers, Ile de la Réunion (2), 1999]
1. Reproduire sur votre copie le tableau ci-dessous et le
compléter en répondant par oui ou par non. Pour la
dernière ligne, on nommera un triangle autre que ceux qui
figurent dans le tableau.
Il ne semble utile de justifier les réponses. Aussi, je me
contente
de remplir le tableau.
 .
.
| Le triangle |
Est-il rectangle ? |
Est-il isocèle ? |
Est-il
équilatéral ? |
| DJH |
Non |
Oui |
Non |
| ACG |
Oui |
Non |
Non |
| AFC |
Non |
Oui |
Oui |
| EHG |
Oui |
Oui |
Non |
| ACJ
ou ... |
Oui |
Non |
Non |
Justifier vos affirmations concernant la nature des triangles AFC
et EHG.

Le triangle EHG est isocèle rectangle en H (car EFGH
est un carré).
Le triangle AFC est équilatéral (en effet, si a
est le côté du cube, d'après le
théorème de Pythagore appliqué
dans les triangles AEF, ABC et ADH, j'obtiens AC
= AF = CF = a x √2) donc isocèle et
non rectangle.
2.a) Sans faire de calcul, dessiner en taille réelle à
l'aide de la règle et du compas le contour de la surface
imprimée. On utilisera des constructions
géométriques annexes (les faire figurer sur la copie).
Expliquer succinctement la construction géométrique.
Je pense à tracer les triangles ERS, EST et ERT
pour
construire les longueurs RS, ST et RT.

.
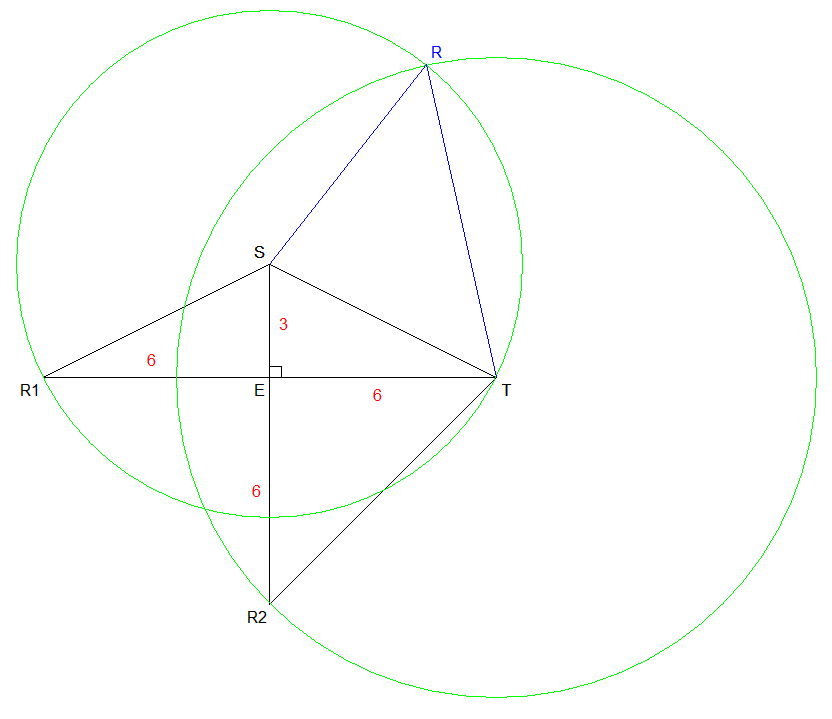
Je construis un segment [R1T] qui mesure 12
cm.
Je construis la médiatrice (d) du segment [R1T]
(à l'aide de la règle non graduée et du compas)
qui coupe le segment [R1T] en le point E
(tel que R1E = ET = 6 cm).
Sur la droite (d), je place les points S et R2
tels que le point E appartienne au segment [R2S],
que R2E = 6 cm et que ES = 3 cm.
Je trace le cercle C1 de centre S et de
rayon [SR1] et le cercle C2 de
centre T
et de rayon [TR2]. Ces cercles C1
et C2 se coupent en deux points dont l'un que je
nomme R.
2.b) Calculer la dimension exacte de la longueur TR.

Le théorème de Pythagore appliqué dans le triangle
TER rectangle en E donne TR
= √(62 + 62) cm = 6
x √2 cm.
2.c) Calculer l'aire exacte en cm2 de la section obtenue.

De la même manière, le théorème de Pythagore
appliqué dans le triangle TES rectangle en E
donne TS = √(62 + 32) cm = 3 x √5 cm et le théorème de Pythagore
appliqué dans le triangle RES rectangle en E
donne RS = √(62 + 32) cm = 3 x √5 cm.
Soit H le pied de la hauteur du triangle TRS issue de S
(et qui est aussi médiane parce que le triangle TRS est
isocèle en S). Le théorème de Pythagore
appliqué dans le triangle SHT rectangle en H
donne SH = √(ST2 - HT2) = √(45 - 18) cm =
3 x √3 cm.
Ainsi, Aire(RST) = (6 x
√2 x 3 x √3)/2 cm2
= 9 x √6 cm2.






