- Solution
[Toulouse,
1999]
1. Montrer que AECF est un parallélogramme.
Je commence par tracer la figure ...

.
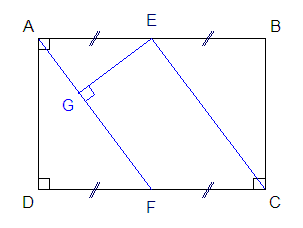
Le quadrilatère ABCD est un rectangle, donc les droites (AE)
et (FC) sont parallèles et de plus, AB = CD,
donc AE = AB/2 = CD/2 = FC. Ainsi, AECF
est un quadrilatère (convexe) ayant
ses côtés opposés [AE] et [FC]
égaux en mesure et parallèles et est
un parallélogramme.
2. Déterminer l'aire du parallélogramme AECF.

Aire(AECF) = AE x
BC = 192 cm2.
3. Calculer la longueur AF.

Le théorème de Pythagore appliqué au triangle ADF
rectangle en D (puisque le
quadrilatère ABCD est un rectangle) donne AF = √(AD2 + DF2) = √(144
+ 256) cm = 20 cm.
4. En déduire la longueur EG.

Je calcule l'aire du parallélogramme AECF d'une seconde
façon Aire(AECF) = AF x EG = 192
cm2. Puis, connaissant AF, je déduis EG = 192/20 cm =
9,6 cm.
5.a) Calculer la valeur exacte du
rayon de la base, puis en
donner une valeur approchée à un mm près par
défaut.

Le cercle de base a donc un périmètre de 20 cm
(son périmètre coïncide
avec la mesure su segment [AF]). Le rayon r de ce
cercle est donc r= 20/(2π) cm = 10/π cm.
Pour le calcul d'une valeur approchée de ce rayon : 3,14
< π < 3,15, puis 3,1 ≤ 10/3,15 < 10/π <
10/3,14 < 3,2 et une valeur
approchée de r au millimètre près par
défaut est 3,1 cm.
5.b) Calculer la valeur exacte de son volume, puis en donner une
valeur approchée à un mm3 près.

Volume(cylindre) = π x
r2 x EG
= π x (10/π)2 x
9,6 cm3 = 960/π cm3
(EG
est bien la hauteur du cylindre car les droites (EG) et (AF)
sont perpendiculaire).
Pour le calcul d'une valeur approchée de ce volume : 3,141592
< π < 3,141593, puis 305,577 ≤ 960/3,141593
< 960/π < 960/3,141592 < 305,578 et une
valeur approchée de Volume(cylindre) au
millimètre cube près par défaut est 305,577
cm3.







