Exercice

Le problème des allumettes de Banach. [10] Un mathématicien se trouve être également fumeur de pipe et il porte à tout moment deux boîtes d'allumettes, une dans chacune de ses poches. Chaque fois qu'il a besoin d'une allumette, il a une chance sur deux d'aller la chercher dans sa poche gauche et autant pour l'autre. Il découvre subittement que la boîte tirée est vide. Les deux boîtes contenaient au départ $N$ allumettes chacune. Quelle est la probabilité $p$ qu'il lui reste $k$ allumettes dans l'autre boîte ? On désigne par $A$ l'événement "le mathématicien découvre que sa poche droite est vide alors qu'il lui reste $k$ allumettes dans l'autre". 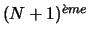Cet événement n'arrive que lorsqu'il choisit la boîte droite pour la $(N+1)^{\grave{e}me}$ fois lors du 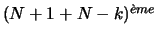$(N+1+N-k)^{\grave{e}me}$ tirage.
Il s'ensuit que 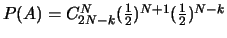$P(A)=C_{2N-k}^{N} (\frac{1}{2})^{N+1}(\frac{1}{2})^{N-k}$, puis $P(A)=C_{2N-k}^{N} (\frac{1}{2})^{2N+1-k}$.
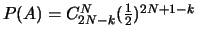Comme la probabilité est la même que ce soit sa poche gauche qui soit vide alors qu'il lui reste $k$ allumettes dans la droite,

$$p=2P(A)=C_{2N-k}^{N} (\frac{1}{2})^{2N-k}.$$