



suivant: Lois discrètes usuelles
monter: Variables aléatoires réelles discrètes
précédent: Inégalité de Bienaymé-Tchebychev
Table des matières
Soient
 ,
,  variables aléatoires réelles discrètes
indépendantes de même loi. Si on note
variables aléatoires réelles discrètes
indépendantes de même loi. Si on note 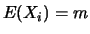 ,
alors :
,
alors :
pour tout  , avec
, avec
 .
Démonstration
On pose
.
Démonstration
On pose
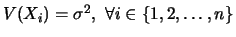 . Dans ce cas,
. Dans ce cas,
 et
et
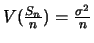 .
.
Ainsi, d'après l'inégalité de Bienaymé-Tchebychev, il résulte :
Puis,
pour tout  , avec
, avec

Vekemans
2002-06-24