Séance 13
D. Vekemans
Maître de Conférences à l'IUFM de Gravelines (59)
Organisation proposée :
1. Partie n°8.
2. Finale R+D vs R+p pour illustrer la technique de triangulation de la Dame dans le cas où le pion est
à une case de la promotion et soutenu par le Roi.
- Les blancs jouent et gagnent.
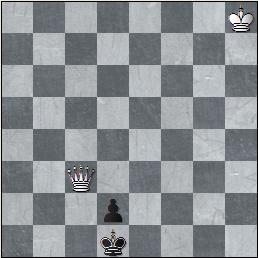 Solution
Solution
- Le cas particulier du pion-Tour. Cette finale est nulle quand le Roi blanc est éloigné, mais gagne quand le
Roi blanc est suffisamment proche.
- Les blancs jouent et gagnent.
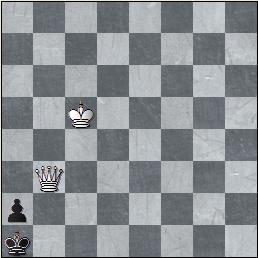 Solution
Solution
- Le cas particulier du pion-Fou. Cette finale est nulle quand le Roi blanc est éloigné, mais gagne quand le
Roi blanc est suffisamment proche.
- Les blancs jouent et gagnent.
 Solution
Solution
3. Finale R+pions vs R+pions dans l'illustration de la force des pions éloignés.
- Les blancs jouent et gagnent.
 Solution
Solution
4. Le mat de Pillsbury.Mat en 4.
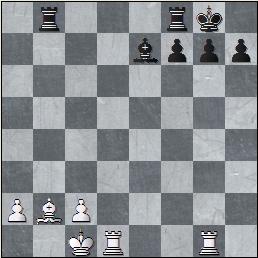 Solution
Solution
Jeu collectif :
- 6. Jeu thématique sans limitation de temps, en faisant tourner les joueurs,
si possible.
- La partie du jour est issue de la variante de Leningrad de la partie Hollandaise qui est caractérisée
par les coups : 1.d4 f5 2.g3 Cf6 3.Fg2 g6 4.Cc3.
- Faire jouer des parties à partir de cette position !
Retour à l'index







