- Exercice [Créteil, Paris,
Versailles, 2004]
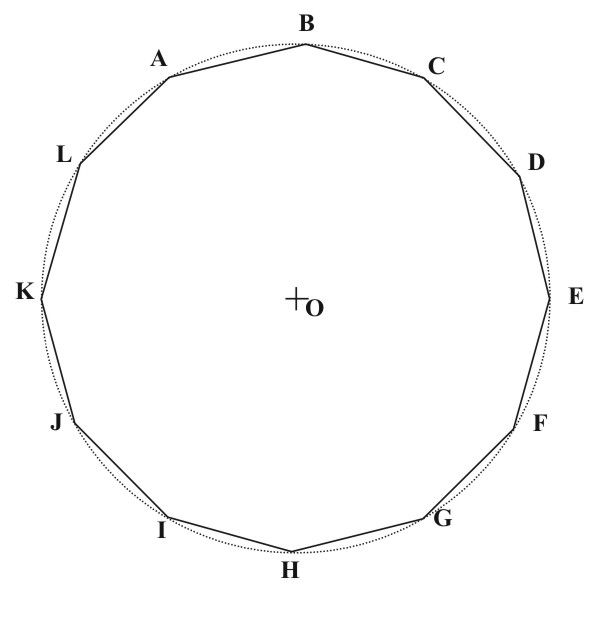
On considère un dodécagone régulier ABCDEFGHIJKL (convexe) inscrit dans un
cercle de centre O et rayon R.
Les côtés [AB], [BC], ..., [KL] et [LA] ont donc la même longueur
et les angles
,
,
...,
ont la même mesure.
1. Quelle est la nature du triangle ACO ?
2. Quelle est la nature du polygone ACEGIK ?
3. La droite (AC) coupe la droite (BO) en M.
Que représente la droite (AM) pour le triangle ABO ?
Exprimer AM en fonction du rayon R du cercle circonscrit au dodécagone.
4. Exprimer l'aire du triangle ABO en fonction du rayon R du cercle.
En déduire que l'aire d'un dodécagone régulier est donnée par la formule :
Aire = 3 x R2 où R représente
le rayon du cercle circonscrit au dodécagone.
5. Quelle est l'aire d'un dodécagone régulier inscrit dans un cercle de
diamètre 18 cm ?
6. Tracer un dodécagone régulier ABCDEFGHIJKL inscrit dans un cercle de
centre O et rayon 6 cm. On utilisera la règle graduée et le compas et
on laissera les traits de construction apparents.
Solution

