- Solution [Martinique,
2000]
1. Pour chacune des affirmations suivantes dire si elle est vraie ou
fausse. Argumenter la réponse. - 1.a) Tous les rectangles
appartiennent à (F).
- 1.b) Certains éléments de (F) sont des
parallélogrammes.

1.a) est FAUX. En général, un rectangle n'a pas ses
diagonales perpendiculaires.
Lorsque les diagonales sont perpendiculaires, le rectangle est alors un
carré.
1.b) est VRAI. Le losange est un parallélogramme qui
possède des diagonales perpendiculaires.
2.a) Quelle est la nature du quadrilatère EFGH ?
Le démontrer.
2.b) Quelle est la condition supplémentaire à
imposer à ABCD pour que EFGH soit un
carré ? Le justifier.
Je commence par tracer la figure.

.
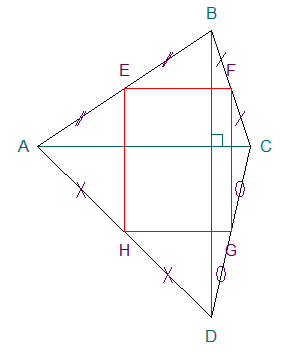
.
EFGH est le parallélogramme de Varignon du
quadrilatère ABCD (voir exercice : le parallélogramme de Varignon).
Ainsi, EFGH est un rectangle. Si, de plus,
les diagonales de ABCD
sont de même mesure, EFGH est un carré.
3.a) Construire à la
règle et au compas, le
quadrilatère ABCD.

- Je trace un segment [AC] tel que AC = 10 cm ;
- je place le point I, milieu du segment [AC], donc
le point I tel que AI = IC = 5 cm ;
- soit C1 le cercle de centre A et de
rayon 6 cm et soit C2 le cercle de centre I
et de rayon 5 cm ;
- soit B l'un des points de concours des cercles C1
et C2 (l'angle intercepte le diamètre [AC]
et
est, par conséquent, droit) et soit B' l'autre ;
- je trace la droite (BB') qui est perpendiculaire à
la droite (AC) (en effet, (AC) est la médiatrice
du segment [BB'] car AB = AB' et IB = IB') ;
- je place le point D sur la droite (BB') de telle
façon que les points D
et B soient de part et d'autre de la droite (AC) et que
BD = 10 cm ;
- je trace le quadrilatère ABCD.
Je propose la figure ...
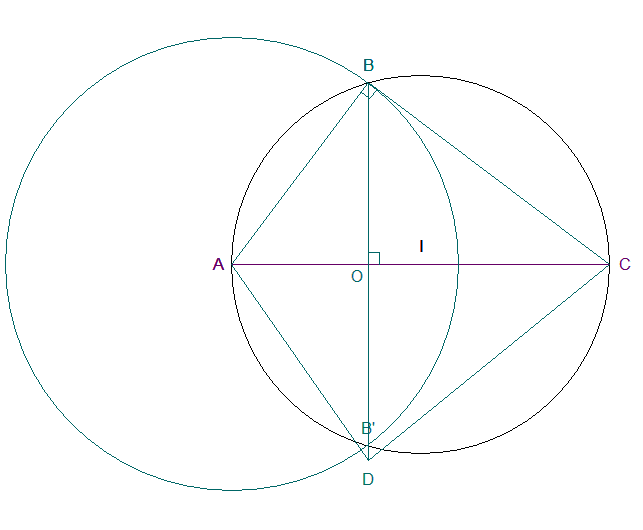
3.b) Si O est le point d'intersection des diagonales [AC]
et [BD], calculer BC puis BO.

Par application du théorème de Pythagore dans le triangle
ABC rectangle en B, je trouve AC2 = AB2
+ BC2, puis BC = √(102
- 62) cm = 8 cm.
Pour trouver OB, je calcule de deux manières l'aire du
triangle ABC : Aire(ABC) = (BA x
BC)/2 = (AC x OB)/2 pour déduire que
OB = (BA x
BC)/AC
= (6 x 8)/10 cm =
4,8 cm.
3.c)i) Montrer que le triangle BOD est rectangle. En
utilisant les résultats précédents, déduire
une construction, en vraie grandeur, de la longueur de l'arête [BD]
du tétraèdre BACD.

L'énoncé nous dit que [OB] est hauteur du
tétraèdre BADC, ce qui implique que la droite (OB)
est orthogonale à toute droite du plan (ACD). En
particulier, la droite (OB) est perpendiculaire à la
droite (OD) et
le triangle OBD est rectangle en O.
Construction utilisant règle non graduée et compas de BD
: - je trace un cercle, un diamètre [MN] de ce cercle
et je prends un point O sur ce cercle distinct de M et
de N (l'angle est alors un angle droit
car il intercepte un diamètre de ce cercle) ;
- je place B sur la demi-droite [OM) en reportant
à l'aide du compas
la longueur OB depuis la figure initiale ;
- je place D sur la demi-droite [ON) en reportant
à l'aide du compas
la longueur OD depuis la figure initiale ;
- je trace le segment [BD].
3.c)ii) Terminer le patron, avec règle et compas, en
laissant apparaître les traces justificatives des constructions.

.
Les tracés relatifs à cette question sont portés
en rouge.
.
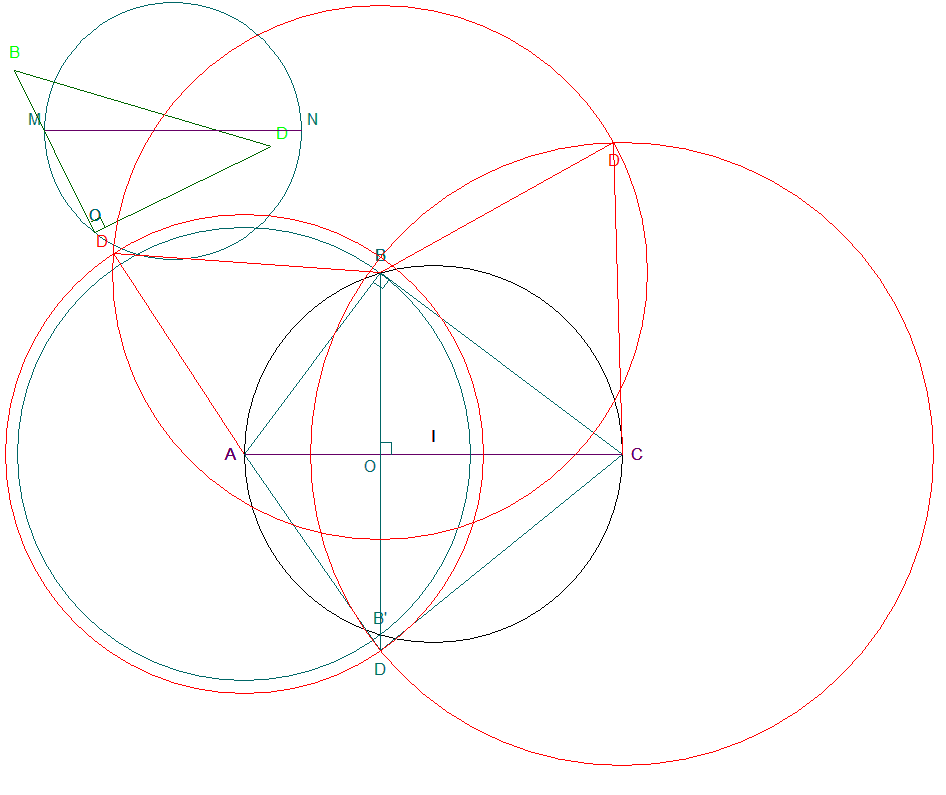
.









