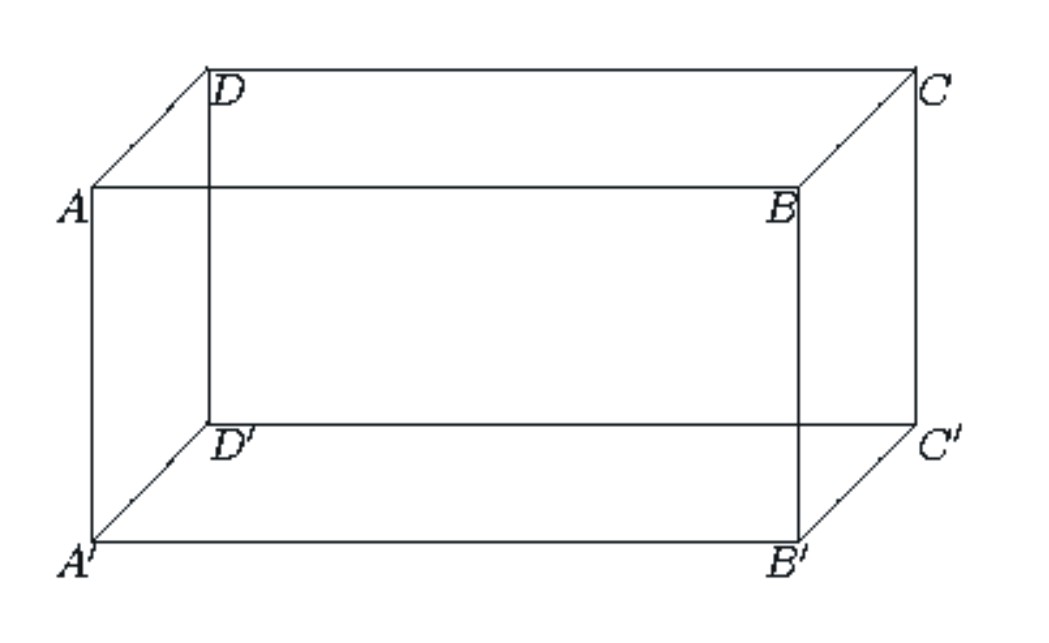
Exercice [Lyon, 1998]

On dispose d'un parallélipipède rectangle dont les côtés ont pour longueurs respectives AB = a, AD = AA' = a/2.

Soient I, J, I' et J' les milieux respectifs des segments [AB], [AD], [A'B'] et [A'D'].

On considère le solide S de sommets B, D, J, I, B', D', J' et I'.

On admettra que les quadrilatères BDD'B' et IJJ'I' sont des rectangles.

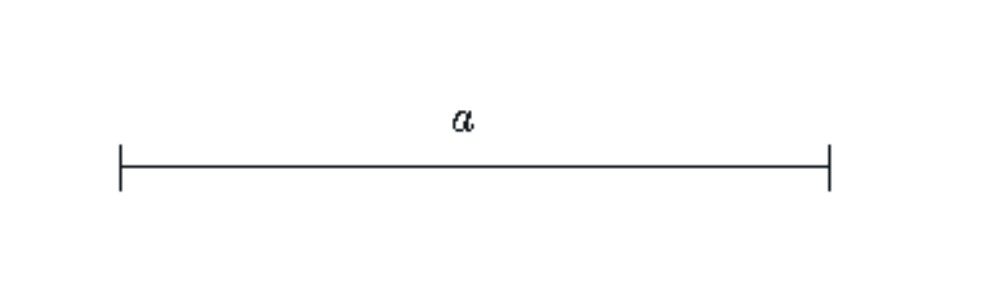
Dans les constructions demandées ci-dessous, on prendra pour longueur a, le segment ci-dessous :

1. Construire le quadrilatère BDJI à la règle non graduée et au compas. Indiquer sa nature. Calculer son aire en fonction de a.

2. Construire un patron du solide S, à la règle graduée et au compas. Ecrire le programme de construction.

3. Quelle est l'aire totale de ce solide exprimée en fonction de a ?

4. Quelle proportion du volume du parallélépipède initial représente le volume de ce solide S ?

Solution