suivant: Caractéristiques
monter: La loi de Poisson
précédent: La loi de Poisson
Table des matières
La variable aléatoire  de Poisson peut prendre une infinité de
valeurs,
de Poisson peut prendre une infinité de
valeurs, 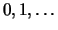 , et
, et 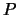 (qui dépend du paramètre
(qui dépend du paramètre 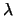 ) est donnée par :
) est donnée par :
On a bien
 suit une loi de Poisson de paramètre
suit une loi de Poisson de paramètre 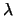 est noté
est noté
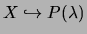 .
.
Vekemans
2002-06-24