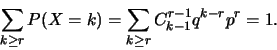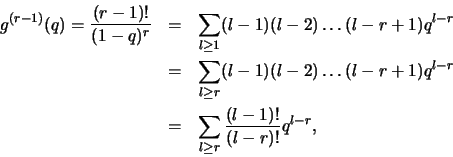suivant: Caractéristiques
monter: La loi binomiale négative
précédent: La loi binomiale négative
Table des matières
Tirage avec remise
La variable aléatoire  binomiale négative peut prendre une infinité de
valeurs,
binomiale négative peut prendre une infinité de
valeurs, 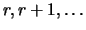 , et
, et 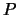 (qui dépend des paramètres
(qui dépend des paramètres  -probabilité de succès
-probabilité de succès 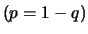 - et
- et 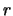 ) est donnée par :
) est donnée par :
On a bien
En effet, si on pose
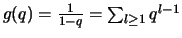 , on obtient
par dérivations successives que
, on obtient
par dérivations successives que
et donc
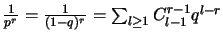 .
.
 suit une loi binomiale négative de paramètres
suit une loi binomiale négative de paramètres 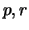 est noté
est noté
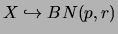 .
En particulier,
.
En particulier,
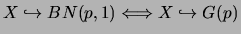 .
.
Vekemans
2002-06-24