



suivant: Fonction de répartition
monter: Variables aléatoires réelles continues
précédent: Remarque
Table des matières
Soit une variable aléatoire réelle continue  ,
,
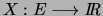 prenant ses
valeurs dans
prenant ses
valeurs dans
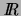 .
On définit la probabilité d'un événement de type
.
On définit la probabilité d'un événement de type 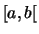 comme la probabilité que la
variable
comme la probabilité que la
variable  prenne sa valeur dans
prenne sa valeur dans 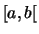 .
La loi de probabilité d'une variable aléatoire réelle continue
.
La loi de probabilité d'une variable aléatoire réelle continue  est
définie par la densité de probabilité
est
définie par la densité de probabilité 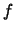 qui est une fonction
positive, continue sauf peut-être en un nombre fini ou dénombrable de
points et qui est telle que
qui est une fonction
positive, continue sauf peut-être en un nombre fini ou dénombrable de
points et qui est telle que
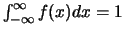 .
La probabilité que l'événement soit de type
.
La probabilité que l'événement soit de type 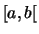 est alors donnée
par la valeur
est alors donnée
par la valeur
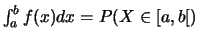 (si
(si 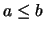 ).
On pourra remarquer que dans le cas d'une variable aléatoire réelle continue,
).
On pourra remarquer que dans le cas d'une variable aléatoire réelle continue,
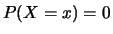 .
.
Vekemans
2002-06-24