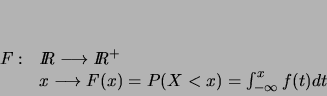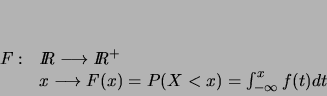suivant: Les moments d'ordre
monter: Variables aléatoires réelles continues
précédent: Lois de probabilités
Table des matières
La fonction de répartition  d'une variable aléatoire continue
d'une variable aléatoire continue  ayant
une densité de probabilité
ayant
une densité de probabilité 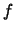 est partout définie et vaut :
est partout définie et vaut :
Propriétés
-
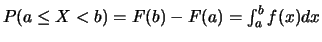
 est une fonction croissante car si
est une fonction croissante car si 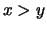 , alors,
, alors,
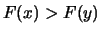
-

-
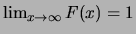
Vekemans
2002-06-24