



suivant: Caractéristiques
monter: La loi uniforme
précédent: La loi uniforme
Table des matières
La densité 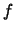 de la variable aléatoire
de la variable aléatoire  uniforme peut prendre deux valeurs, 0 et
uniforme peut prendre deux valeurs, 0 et
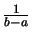 où
où  et
et 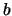 sont deux constantes données (
sont deux constantes données (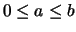 ). Elle est définie par :
). Elle est définie par :
On a bien
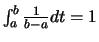 .
La fonction de répartition
.
La fonction de répartition  de la précédente variable aléatoire
de la précédente variable aléatoire  est donnée par
est donnée par
Vekemans
2002-06-24
![\begin{displaymath}f(x)= \left\{
\begin{array}{ll}
\frac{1}{b-a} & si x \in [a,b]\\
0 & sinon
\end{array}.
\right.\end{displaymath}](img705.png)
![\begin{displaymath}f(x)= \left\{
\begin{array}{ll}
\frac{1}{b-a} & si x \in [a,b]\\
0 & sinon
\end{array}.
\right.\end{displaymath}](img705.png)
![\begin{displaymath}F(x)=
\left\{
\begin{array}{ll}
\frac{x-a}{b-a} & si x...
...b]\\
0 & si x<a\\
1 & si x>b
\end{array}.
\right.\end{displaymath}](img707.png)