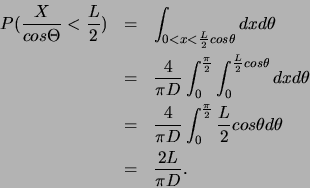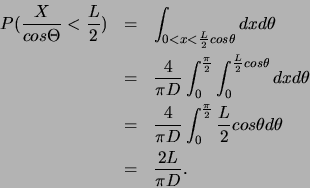suivant: La loi de Gamma
monter: La loi uniforme
précédent: Caractéristiques
Table des matières
Problème de l'aiguille de Buffon. [10] Sur une table, on trace
des lignes parallèles espacées d'un écart  les unes des autres. On y
jette une aiguille de longueur
les unes des autres. On y
jette une aiguille de longueur 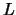 , avec
, avec 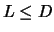 . Quelle est la probabilité
que l'aiguille coupe une ligne (l'alternative étant que l'aiguille soit
complètement située dans une des bandes délimitées par les lignes).
Correction :
On repère la position de l'aiguille grâce à la distance entre le centre
de celle-ci et la parallèle la plus proche, et grâce à l'angle
. Quelle est la probabilité
que l'aiguille coupe une ligne (l'alternative étant que l'aiguille soit
complètement située dans une des bandes délimitées par les lignes).
Correction :
On repère la position de l'aiguille grâce à la distance entre le centre
de celle-ci et la parallèle la plus proche, et grâce à l'angle 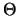 entre l'aiguille et une perpendiculaire aux lignes. L'aiguille coupe une
ligne si
entre l'aiguille et une perpendiculaire aux lignes. L'aiguille coupe une
ligne si
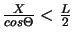 . La variable
. La variable  varie entre
varie entre 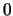 et
et
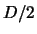 et
et 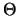 entre
entre 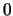 et
et 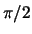 . On admet que les variables
. On admet que les variables  et
et
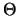 sont uniformément réparties et indépendantes. Ainsi,
sont uniformément réparties et indépendantes. Ainsi,
Vekemans
2002-06-24