



suivant: Caractéristiques
monter: La loi de Gamma
précédent: La loi de Gamma
Table des matières
La variable aléatoire  de Gamma est
donnée par sa densité
de Gamma est
donnée par sa densité 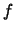 telle que :
telle que :
où
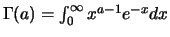 et
et 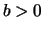 (on a en
particulier
(on a en
particulier
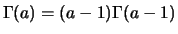 et
et
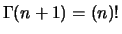 ,
,
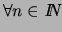 ).
On a bien
).
On a bien
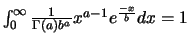 .
.
 suit une loi de Gamma de paramètres
suit une loi de Gamma de paramètres 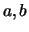 est noté
est noté
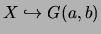 .
Un cas particulier de cette loi est la loi exponentielle où l'on impose
.
Un cas particulier de cette loi est la loi exponentielle où l'on impose 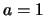 et
et
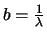
Vekemans
2002-06-24

