



suivant: La loi de Laplace-Gauss
monter: La loi de Gamma
précédent: Caractéristiques
Table des matières
[10] On suppose que la durée d'une conversation téléphonique,
mesurée en minutes, est une variable aléatoire exponentielle de paramètre
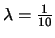 . J'arrive à une cabine et quelqu'un passe juste avant
moi. Avec quelle probabilité dois-je attendre
. J'arrive à une cabine et quelqu'un passe juste avant
moi. Avec quelle probabilité dois-je attendre
- plus de 10 minutes.
Réponse :  désigne la durée de la conversation de la personne qui m'a
devancé.
désigne la durée de la conversation de la personne qui m'a
devancé.
![$P(X>10)=\int_{10}^{\infty} \frac{1}{10} e^{\frac{-x}{10}}dx
=[-e^{\frac{-x}{10}}]_{10}^{\infty}=\frac{1}{e}.$](img736.png)
- entre 10 et 20 minutes.
Réponse :
![$P(10<X<20)=\int_{10}^{20} \frac{1}{10} e^{\frac{-x}{10}}dx
=[-e^{\frac{-x}{10}}]_{10}^{20}=\frac{1}{e}-\frac{1}{e^2}.$](img737.png)
Vekemans
2002-06-24