



suivant: Caractéristiques
monter: La loi de Laplace-Gauss
précédent: La loi de Laplace-Gauss
Table des matières
La variable aléatoire  normale est
donnée par sa densité
normale est
donnée par sa densité 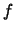 telle que :
telle que :
où
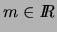 et
et
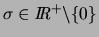 .
On a bien
.
On a bien
En effet,
De plus, on remarquera que 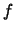 est symétrique par rapport à
est symétrique par rapport à 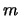 puisque
puisque
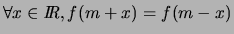 .
.
 suit une loi normale de paramètres
suit une loi normale de paramètres 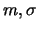 est noté
est noté
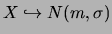 .
.
Vekemans
2002-06-24
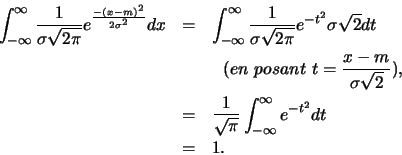
![\begin{eqnarray*}
% latex2html id marker 2370
\left( \int_{-\infty}^{\infty}
...
...\\
&=& 2\pi [\frac{-1}{2}e^{-r^2}]_0^{\infty}\\
&=& \pi \\
\end{eqnarray*}](img742.png)