



suivant: Valeurs remarquables pour
monter: La loi de Laplace-Gauss
précédent: Caractéristiques
Table des matières
On appelle loi normale centrée réduite la loi normale de paramètres 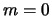 et
et 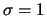 .
Ainsi, la densité de probabilité devient
.
Ainsi, la densité de probabilité devient
La fonction de répartition  s'écrit
s'écrit
La courbe représentative de  passe par le point de coordonnées
(0,
passe par le point de coordonnées
(0,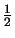 ), possède une asymptote au voisinage de
), possède une asymptote au voisinage de 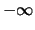 d'équation
d'équation 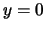 (et une asymptote au voisinage de
(et une asymptote au voisinage de  d'équation
d'équation 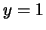 ) et est symétrique par rapport au point de coordonnées
(0,
) et est symétrique par rapport au point de coordonnées
(0,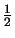 ).
On remarque que si
).
On remarque que si
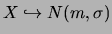 (loi normale), alors,
(loi normale), alors,
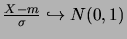 (loi normale centrée réduite).
Propriétés
Ces propriétés servent à utiliser la table de la loi normale centrée réduite ne donnant qu'une partie des valeurs.
On note
(loi normale centrée réduite).
Propriétés
Ces propriétés servent à utiliser la table de la loi normale centrée réduite ne donnant qu'une partie des valeurs.
On note
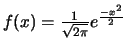 .
.
-
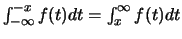
En effet,
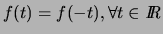 .
.
-
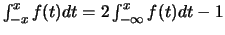
En effet,
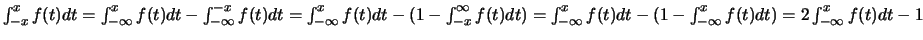 .
.
Vekemans
2002-06-24
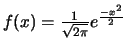 .
.