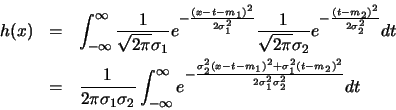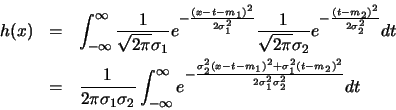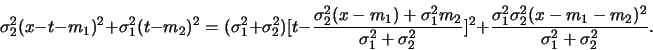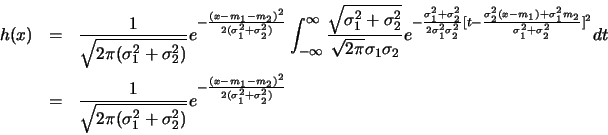suivant: Approximation de la loi
monter: La loi de Laplace-Gauss
précédent: Valeurs remarquables pour
Table des matières
Si
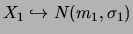 et si
et si
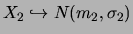 sont indépendantes, alors
sont indépendantes, alors
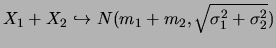 .
Démonstration
La densité de probabilité de
.
Démonstration
La densité de probabilité de 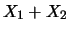 est
est
Ensuite, le polynôme
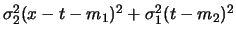 de degré deux en
de degré deux en 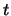 est mis sous forme canonique :
est mis sous forme canonique :
Ainsi,
Et, le résultat demandé est ainsi prouvé.
Vekemans
2002-06-24