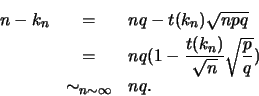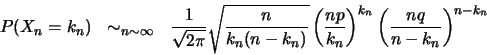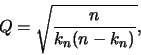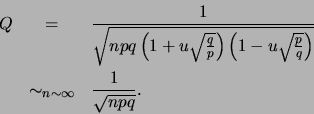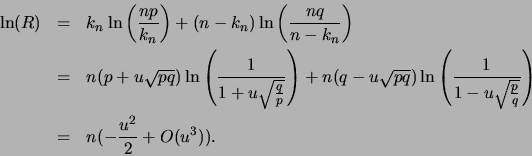suivant: Le théorème central limit
monter: La loi de Laplace-Gauss
précédent: Additivité de deux lois
Table des matières
Soit ![$p\in ]0,1[$](img774.png) .
Soit
.
Soit 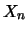 une suite de variables aléatoires suivant la loi binomiale de paramètres
une suite de variables aléatoires suivant la loi binomiale de paramètres  (
(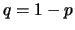 ) et
) et  . Ainsi,
. Ainsi,
Ainsi, on a :
En d'autres termes, la loi binomiale approche la loi normale.
Idée de la démonstration
Rappel de la formule de Stirling :
On pose
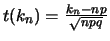 .
On a
.
On a
De même,
En appliquant la formule de Stirling,
On pose alors
et
On obtient
et
Ensuite,
Il s'ensuit :
Ensuite, en admettant qu'on peut faire la somme infinie de ces équivalents (le démontrer n'est pas chose aisée), on obtient :




suivant: Le théorème central limit
monter: La loi de Laplace-Gauss
précédent: Additivité de deux lois
Table des matières
Vekemans
2002-06-24
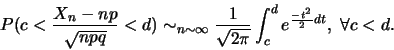
![\begin{eqnarray*}
k_n&=&np+t(k_n)\sqrt{npq}\\
&=&np(1+\frac{t(k_n)}{\sqrt{n}}...
...\infty} \frac{t(k_n)}{\sqrt{n}}=0 puisque t(k_n)\in [c,d]).
\end{eqnarray*}](img781.png)