



suivant: Exercice
monter: La loi de Laplace-Gauss
précédent: Approximation de la loi
Table des matières
Le théorème de De Moivre-Laplace est un cas particulier du théorème suivant.
Enoncé
Soient
 ,
,  variables aléatoires réelles indépendantes
de même loi. Si on note
variables aléatoires réelles indépendantes
de même loi. Si on note 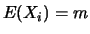 et
et
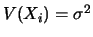 , alors :
, alors :
lorsque 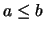 et
et

ou, avec une conclusion formulée autrement,
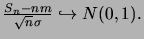 Ce théorème n'est pas démontré.
Ce théorème n'est pas démontré.
Vekemans
2002-06-24