



suivant: Conséquences et propriétés
monter: Les axiomes du calcul
précédent: Les axiomes du calcul
Table des matières
Soit  un ensemble fondamental composé d'un ensemble dénombrable
d'événements élémentaires. Les événements élémentaires
possibles sont
un ensemble fondamental composé d'un ensemble dénombrable
d'événements élémentaires. Les événements élémentaires
possibles sont
 .
.
Soit 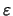 le référentiel associé
à l'ensemble fondamental
le référentiel associé
à l'ensemble fondamental  (i.e. les événements
(i.e. les événements
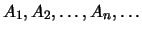 de
de
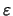 peuvent s'écrire comme réunion dénombrable
d'événements élémentaires
peuvent s'écrire comme réunion dénombrable
d'événements élémentaires
 de
de  ).
).
On définit la fonction 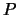 :
:
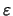
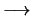
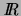 telle que
telle que 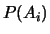 désigne
la probabilité de l'événement
désigne
la probabilité de l'événement 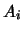 si les axiomes suivants sont
vérifiés :
si les axiomes suivants sont
vérifiés :
-
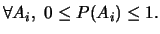
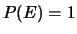 ,
,
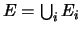 est appelé événement certain.
est appelé événement certain.
-
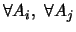 tels que
tels que
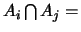 Ø
(événements incompatibles), on a
Ø
(événements incompatibles), on a
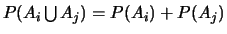 .
.
Vekemans
2002-06-24