



suivant: Lien entre la probabilité
monter: Les axiomes du calcul
précédent: Enoncé
Table des matières
- Si Ø désigne l'événement impossible, on a
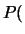 Ø
Ø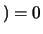 .
Démonstration
.
Démonstration 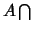 Ø
Ø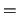 Ø
Ø
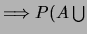 Ø
Ø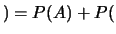 Ø
Ø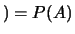
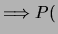 Ø
Ø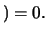
- Si
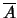 est l'événement contraire de
est l'événement contraire de  , alors
, alors
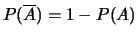 .
Démonstration
.
Démonstration
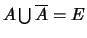 et
et
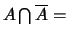 Ø,
Ø,
donc
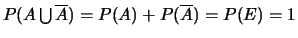 ,
et donc
,
et donc
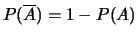 .
.
- Soient
 et
et 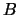 quelconques, alors
quelconques, alors
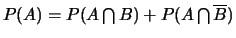 .
Démonstration
.
Démonstration
 et
et
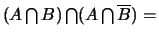 Ø,
Ø,
donc
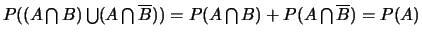 .
.
- Si
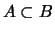 , on a
, on a
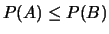 .
Démonstration
.
Démonstration
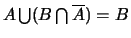 car
car 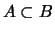 et
et
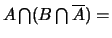 Ø,
Ø,
donc
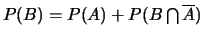 et puis
et puis
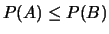 .
.
Vekemans
2002-06-24