



suivant: Exercice
monter: Les axiomes du calcul
précédent: Conséquences et propriétés
Table des matières
Enoncé du théorème
Démonstration
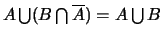 et
et
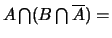 Ø,
Ø,
donc
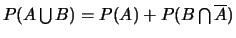 .
.
Or
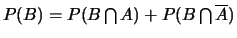 , donc, directement,
, donc, directement,
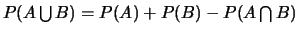 .
Remarque On pourra constater cette propriété sur
les exercices 2.5.4. et 2.5.5.
.
Remarque On pourra constater cette propriété sur
les exercices 2.5.4. et 2.5.5.
Vekemans
2002-06-24