



suivant: Espaces probabilisés
monter: Statistique descriptive
précédent: Second exercice
Table des matières
Cas d'une entrée double discrète.
On donne un tableau statistique à double entrée X et Y. Pour l'observation
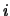 , X prend la valeur
, X prend la valeur 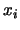 , Y prend la valeur
, Y prend la valeur 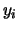 , et ceci dénombré
, et ceci dénombré
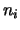 fois.
fois.
- Donner les moyennes à
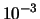 près.
près.
- Donner les variances à
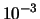 près.
près.
- Donner la covariance à
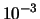 près.
près.
- Donner la droite de régression de Y en fonction de X.
- Donner le coefficient de corrélation et conclure quant à la qualité
de cet ajustement.
- Donner une estimation de Y, lorsque X prend la valeur 1, à
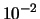 près.
près.
Solution :
-
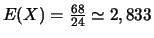 .
.
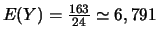 .
.
-
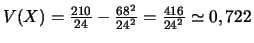 .
.
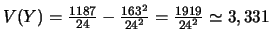 .
.
-
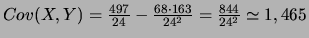 .
.
-
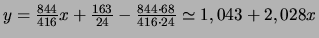 .
.
-
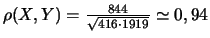 .
.
Très bon ajustement.
- Si
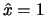 , alors
, alors
 .
.
Vekemans
2002-06-24

