



suivant: Troisième exercice
monter: Statistique descriptive
précédent: Premier exercice
Table des matières
Cas d'une entrée simple continue.
Le taux de triglycérides est observé chez 250 hommes de 20 à 30 ans.
On relève les résultats suivants :
- Donner la classe modale (i.e. la classe la plus fréquente).
- Tracer la fonction cumulative croissante des fréquences relatives.
- Donner la médiane et l'écart interquartile.
Aide : pour avoir des classes de même longueur, on remplacera dans le calcul
de la moyenne et de l'écart-type, la première par
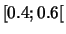 et la
dernière par
et la
dernière par 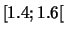 .
.
- Donner la moyenne des observations avec 4 décimales.
- Donner l'écart-type des observations avec 4 décimales.
Solution :
- Classe modale :
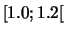 .
.
- Tracer.
-
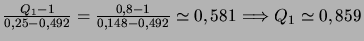 .
.
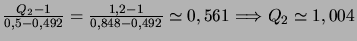 (médiane).
(médiane).
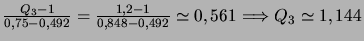 .
.
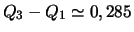 (écart interquartile).
(écart interquartile).
- Moyenne :
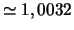 .
.
- Ecart-type :
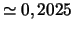 .
.
Vekemans
2002-06-24


