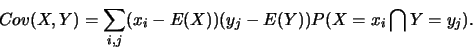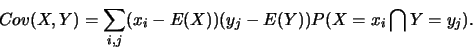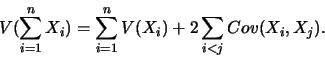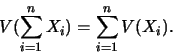suivant: Droite de régression et
monter: Covariance, régression et corrélation
précédent: Covariance, régression et corrélation
Table des matières
Lorsque les quantités
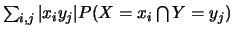 ,
,
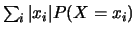 et
et
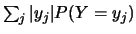 sont définies,
on appelle covariance de deux variables aléatoires réelles discrètes
sont définies,
on appelle covariance de deux variables aléatoires réelles discrètes
 et
et  , et on note
, et on note 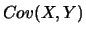 la quantité :
la quantité :
La covariance de deux variables aléatoires réelles discrètes indépendantes est nulle, et on
a :
En retournant à la formule donnant la variance de la somme de deux
variables aléatoires réelles discrètes, on trouve :
En généralisant à  variables,
variables,
Et ensuite, si les variables
sont indépendantes deux à deux :
Vekemans
2002-06-24