



suivant: Covariance conditionnelle
monter: Covariance, régression et corrélation
précédent: Covariance
Table des matières
On nomme coefficient de corrélation et l'on note 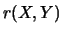 la quantité
la quantité
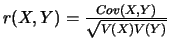 .
Soient
.
Soient  et
et  deux variables aléatoires réelles discrètes.
deux variables aléatoires réelles discrètes.
La droite D d'équation 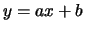 où
où
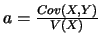 et
et 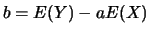 , est
appelée la droite de régression linéaire de
, est
appelée la droite de régression linéaire de  par rapport à
par rapport à  ;
cette droite D minimise la somme des carrés des écarts en ordonnée entre
les représentations graphiques des valeurs et leurs projections sur D selon (0y), pondérés de leur probabilités.
Démonstration
Il nous faut minimiser en fonction de
;
cette droite D minimise la somme des carrés des écarts en ordonnée entre
les représentations graphiques des valeurs et leurs projections sur D selon (0y), pondérés de leur probabilités.
Démonstration
Il nous faut minimiser en fonction de  et
et 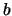 ,
,
Cette quantité est minimale lorsque 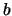 est tel que
est tel que
 (i.e. le point moyen appartient à cette droite) et lorsque
(i.e. le point moyen appartient à cette droite) et lorsque  est tel que
est tel que
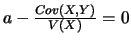 . Dans ce cas, le minimum est
. Dans ce cas, le minimum est
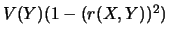 .
Conséquence
Les points sont alignés si et seulement si
.
Conséquence
Les points sont alignés si et seulement si 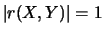 .
La droite D'
d'équation
.
La droite D'
d'équation 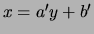 où
où
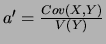 et
et
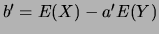 , est appelée la droite de régression linéaire de
, est appelée la droite de régression linéaire de  par rapport à
par rapport à  ; cette droite D' minimise la somme des carrés des écarts en abscisse entre les représentations graphiques des valeurs et leurs projections sur D' selon (0x), pondérés de leur probabilités.
Conséquences
; cette droite D' minimise la somme des carrés des écarts en abscisse entre les représentations graphiques des valeurs et leurs projections sur D' selon (0x), pondérés de leur probabilités.
Conséquences
- Le point de coordonnées
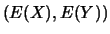 est commun aux deux droites D et D'.
est commun aux deux droites D et D'.
- Les deux droites sont confondues si et seulement si
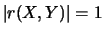 .
.
Lorsque le coefficient de corrélation est proche de 1 en valeur absolue, on parle de bon ajustement et, dans ce cas, les droites D et D' sont presque confondues.
Inversement, lorsque ce coefficient est proche de 0, on parle de mauvais ajustement, et dans ce cas, les variables  et
et  sont presque non covariées (i.e. elles n'ont rien à voir entre-elles).
Ainsi, ce coefficient rend compte de la validité de la régression linéaire.
Propriété
Si
sont presque non covariées (i.e. elles n'ont rien à voir entre-elles).
Ainsi, ce coefficient rend compte de la validité de la régression linéaire.
Propriété
Si 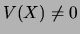 et si
et si 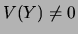 , alors
, alors
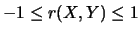 .
En effet,
.
En effet,
et donc 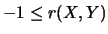 .
Puis,
.
Puis,
et donc 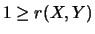 .
.




suivant: Covariance conditionnelle
monter: Covariance, régression et corrélation
précédent: Covariance
Table des matières
Vekemans
2002-06-24
![\begin{eqnarray*}
&&\sum_{i,j}(y_j-ax_i-b)^2P(X=x_i\bigcap Y=y_j)\\
&=&[a^2V(...
...-\frac{Cov(X,Y)}{V(X)}]^2+[(E(Y)-aE(X)-b)^2]+V(Y)(1-(r(X,Y))^2)
\end{eqnarray*}](img357.png)
![\begin{eqnarray*}
&&\sum_{i,j}(y_j-ax_i-b)^2P(X=x_i\bigcap Y=y_j)\\
&=&[a^2V(...
...-\frac{Cov(X,Y)}{V(X)}]^2+[(E(Y)-aE(X)-b)^2]+V(Y)(1-(r(X,Y))^2)
\end{eqnarray*}](img357.png)
![\begin{eqnarray*}
0 \leq V(\frac{X}{\sigma(X)}+ \frac{Y}{\sigma(Y)})&=&
\frac{...
...)^2}+2\frac{Cov(X,Y)}
{\sigma(X) \sigma(Y)}\\
&=&2[1+r(X,Y)]
\end{eqnarray*}](img369.png)
![\begin{eqnarray*}
0 \leq V(\frac{X}{\sigma(X)}- \frac{Y}{\sigma(Y)})&=&
\frac{...
...)^2}-2\frac{Cov(X,Y)}
{\sigma(X) \sigma(Y)}\\
&=&2[1-r(X,Y)]
\end{eqnarray*}](img371.png)