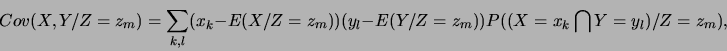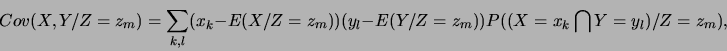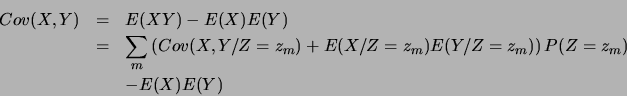suivant: Exercice
monter: Covariance, régression et corrélation
précédent: Droite de régression et
Table des matières
Soient  ,
,  et
et 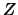 trois variables aléatoires réelles discrètes. On définit
alors la covariance conditionnelle de
trois variables aléatoires réelles discrètes. On définit
alors la covariance conditionnelle de 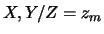 par :
par :
ou par :
d'après une propriété citée plus haut, relative à la covariance.
Il s'ensuit que nous obtenons le résultat suivant :
Démonstration
On a :
Donc,
Vekemans
2002-06-24