



suivant: Exercice
monter: Covariance, régression et corrélation
précédent: Covariance conditionnelle
Table des matières
Soit  la variable aléatoire dont la valeur est le nombre de points
indiqués par la face supérieure d'un dé à 6
faces non pipé, lors de son lancer.
On considère une urne contenant 6 boules indiscernables au toucher dont 3 noires, 2 blanches et 1 verte.
On extrait au hasard une boule de l'urne.
Si celle-ci est noire
la variable aléatoire dont la valeur est le nombre de points
indiqués par la face supérieure d'un dé à 6
faces non pipé, lors de son lancer.
On considère une urne contenant 6 boules indiscernables au toucher dont 3 noires, 2 blanches et 1 verte.
On extrait au hasard une boule de l'urne.
Si celle-ci est noire  , on lance 3 dés, si elle est blanche
, on lance 3 dés, si elle est blanche 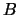 , 2 dés et si elle est verte
, 2 dés et si elle est verte 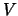 , un dé.
Le jeu coûte 8F et rapporte 1F par nombre
, un dé.
Le jeu coûte 8F et rapporte 1F par nombre  de point(s) indiqué(s) par le(s) dé(s). Combien peut-on espérer gagner
de point(s) indiqué(s) par le(s) dé(s). Combien peut-on espérer gagner 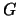 ou perdre au cours d'une partie de ce jeu ?
Solution :
ou perdre au cours d'une partie de ce jeu ?
Solution :
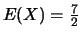 ;
;
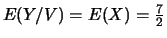 ;
;
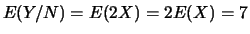 ;
;
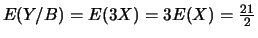 ;
;
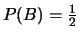 ;
;
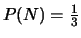 ;
;
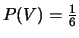 .
Ainsi,
.
Ainsi,
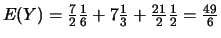 .
Et,
.
Et,
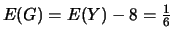 .
.
Vekemans
2002-06-24