



suivant: Exercice
monter: Covariance, régression et corrélation
précédent: Exercice
Table des matières
Soit  la variable aléatoire dont la valeur est le nombre de points
indiqués par la face supérieure d'un dé à 6
faces non pipé, lors de son lancer.
On appelle
la variable aléatoire dont la valeur est le nombre de points
indiqués par la face supérieure d'un dé à 6
faces non pipé, lors de son lancer.
On appelle  le résultat obtenu à ce lancer.
Soit
le résultat obtenu à ce lancer.
Soit  la variable aléatoire totalisant le nombre de fois que l'on obtient
pile en jetant
la variable aléatoire totalisant le nombre de fois que l'on obtient
pile en jetant  pièces de monnaie équilibrées.
Calculer
pièces de monnaie équilibrées.
Calculer  ,
, 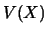 ,
, 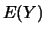 ,
, 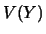 , et
, et 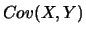 .
Solution : Pour calculer
.
Solution : Pour calculer  et
et 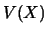 , on utilise
, on utilise
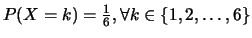 , et il s'ensuit que
, et il s'ensuit que
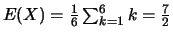 ;
;
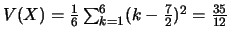 .
Afin d'obtenir
.
Afin d'obtenir 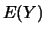 et
et 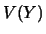 , on utilise
, on utilise
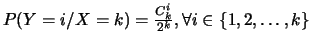 , et il s'ensuit que
, et il s'ensuit que
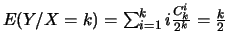 et que
et que
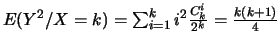 puis que
puis que
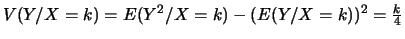 .
En poursuivant,
.
En poursuivant,
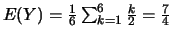 ;
;
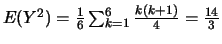 et donc
et donc
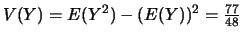 ou encore,
ou encore,
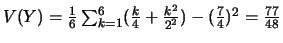 , d'après la formule de la variance conditionnelle.
Par ailleurs, il est évident que
, d'après la formule de la variance conditionnelle.
Par ailleurs, il est évident que
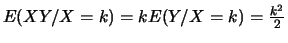 et que
et que
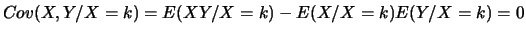 .
Puis
.
Puis
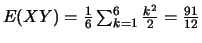 , et donc
, et donc
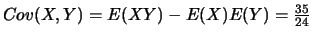 ou encore,
ou encore,
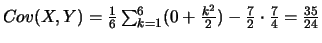 , d'après la formule de la covariance conditionnelle.
Donner les deux droites de régression. Expliquer.
Solution :
, d'après la formule de la covariance conditionnelle.
Donner les deux droites de régression. Expliquer.
Solution :
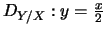 ;
;
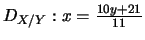 ;
;
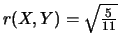 . (mauvais ajustement linéaire)
Tracer et explications ; donner un nuage statistique de points ayant les mêmes caractéristiques.
. (mauvais ajustement linéaire)
Tracer et explications ; donner un nuage statistique de points ayant les mêmes caractéristiques.
Vekemans
2002-06-24