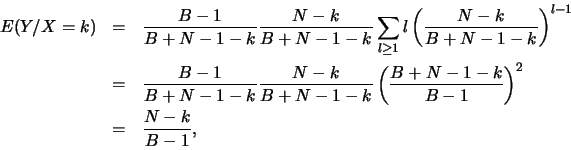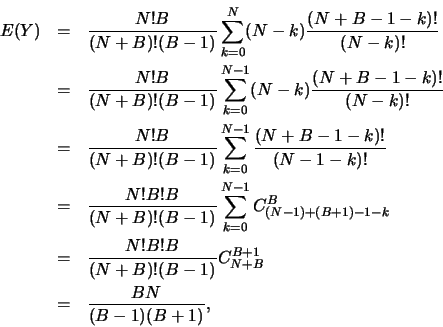suivant: Inégalité de Markov
monter: Covariance, régression et corrélation
précédent: Exercice
Table des matières
On considère une urne contenant  (on suppose
(on suppose 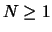 ) boules noires et
) boules noires et
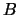 (on suppose
(on suppose 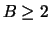 ) boules blanches, toutes indiscernables.
Le joueur A extrait des boules de l'urne, sans les remettre, une à une,
jusqu'à tirer une boule blanche.
Ensuite, le joueur B tire des boules de l'urne, en les remettant, une à une,
jusqu'à tirer une boule blanche.
Le vainqueur du jeu est celui qui a tiré le plus de boules noires.
Qui a le plus de chance de gagner ? Si le joueur B parie
) boules blanches, toutes indiscernables.
Le joueur A extrait des boules de l'urne, sans les remettre, une à une,
jusqu'à tirer une boule blanche.
Ensuite, le joueur B tire des boules de l'urne, en les remettant, une à une,
jusqu'à tirer une boule blanche.
Le vainqueur du jeu est celui qui a tiré le plus de boules noires.
Qui a le plus de chance de gagner ? Si le joueur B parie 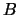 mises alors que
le joueur A ne parie que
mises alors que
le joueur A ne parie que 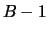 mises, le pari est-il équilibré ?
Solution :
mises, le pari est-il équilibré ?
Solution :
 Et donc,
Et donc,
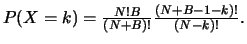 On remarque que
On remarque que
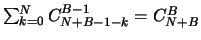 .
Ainsi,
.
Ainsi,
et donc
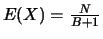 .
D'autre part,
.
D'autre part,
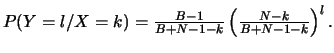 Donc
Donc
puis,
Il s'ensuit que le joueur B a plus de chance de gagner que le joueur A car
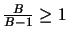 . Par contre, le pari dont la cote est
fixée plus haut est équitable.
. Par contre, le pari dont la cote est
fixée plus haut est équitable.
Vekemans
2002-06-24
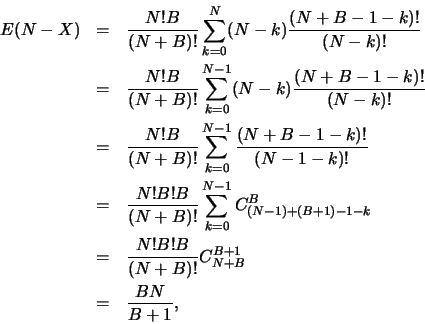
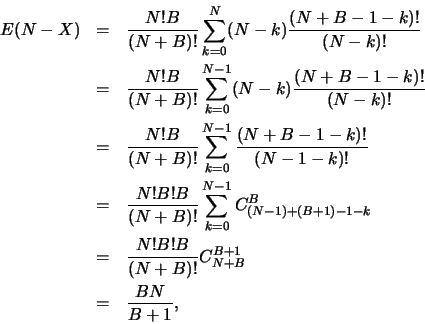
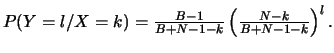 Donc
Donc