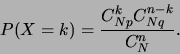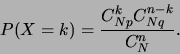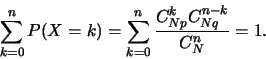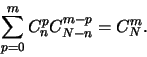suivant: Caractéristiques
monter: La loi hypergéométrique
précédent: La loi hypergéométrique
Table des matières
Définition
La variable aléatoire  hypergéométrique peut prendre
hypergéométrique peut prendre 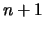 valeurs,
valeurs,
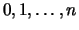 , et
, et 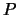 (qui dépend des paramètres
(qui dépend des paramètres  -population totale-,
-population totale-,  -nombre d'échantillons dans la population totale- et
-nombre d'échantillons dans la population totale- et  -probabilité de succès
-probabilité de succès 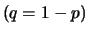 -) est donnée par :
-) est donnée par :
Montrons que,
Ceci revient à montrer que
Par récurrence sur  ,
,
- Pour
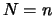 ,
,
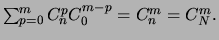
-
 suit une loi hypergéométrique de paramètres
suit une loi hypergéométrique de paramètres 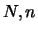 et
et est noté
est noté
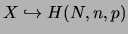 .
.
Vekemans
2002-06-24