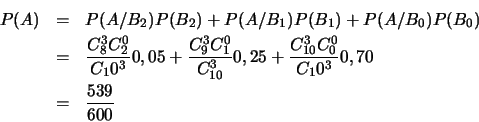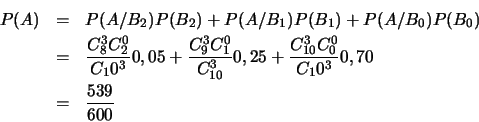suivant: La loi géométrique
monter: La loi hypergéométrique
précédent: Approximation de la loi
Table des matières
Un électricien achète des composants par paquets de 10. Sa technique de
contrôle est de n'examiner que trois des composants, tirés au hasard dans
le paquet et de n'acheter le lot des 10 paquets que si les trois composants
examinés sont sans défaut. Si 5 pourcents des paquets contiennent deux
composants à malfaçon, si 25 pourcents n'en contiennent qu'un et si 70
pourcents n'en contiennent aucun, quelle est la probabilité que l'électricien
achète un paquet.
Solution : On note  l'événement "l'électricien
achète un paquet" et
l'événement "l'électricien
achète un paquet" et 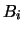 l'événement "le paquet contient
l'événement "le paquet contient 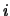 composants
à malfaçon". On a
composants
à malfaçon". On a
Vekemans
2002-06-24