



suivant: Additivité de deux variables
monter: La loi de Poisson
précédent: Caractéristiques
Table des matières
La loi binomiale approche la loi de Poisson lorsque  tend vers
l'infini, pour
tend vers
l'infini, pour
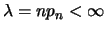 .
On suppose donc que
.
On suppose donc que
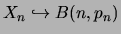 et donc
et donc
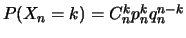 .
Nous nous proposons de montrer que sous les conditions précédentes,
.
Nous nous proposons de montrer que sous les conditions précédentes,
On a :
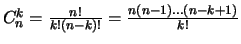
Par ailleurs,
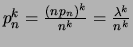
et
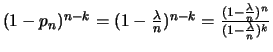
Donc
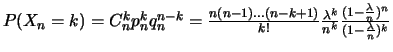 .
.
Or
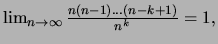
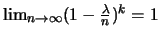
et
 (par passage au
logarithme).
(par passage au
logarithme).
Et donc
 lorsque
lorsque
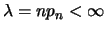 .
.
Vekemans
2002-06-24
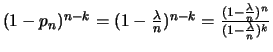
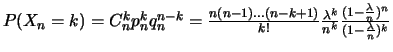 .
.