



suivant: L'espérance mathématique
monter: Les moments d'ordre
précédent: Les moments d'ordre
Table des matières
Soit  une variable aléatoire réelle continue de densité
une variable aléatoire réelle continue de densité 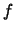 .
Exprimer la densité de
.
Exprimer la densité de 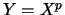 ,
,
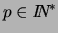 .
Montrer que si
.
Montrer que si
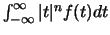 existe, alors :
existe, alors :
Premier cas :  impair.
impair.
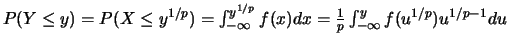 et la densité de
et la densité de  est
est
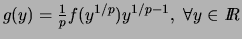 .
Il s'ensuit :
.
Il s'ensuit :
Second cas :  pair.
pair.
![$P(Y\leq y)=P(-y^{1/p} \leq X \leq y^{1/p})=
\int_{0}^{y^{1/p}} (f(x)+f(-x)) dx
=\frac{1}{p} \int_{0}^{y} [f(u^{1/p})+ f(-u^{1/p}) ] u^{1/p-1} du$](img600.png) et la densité de
et la densité de  est
est
![% latex2html id marker 5061
$g(y)=\frac{1}{p} [f(y^{1/p})+ f(-y^{1/p}) ] y^{1/p-1}, \forall y \in \hbox{\it I\hskip -2pt R}^+$](img601.png) et
et
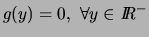 .
Il s'ensuit :
.
Il s'ensuit :
Application directe : Si  a pour densité
a pour densité
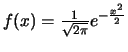 , quelle est la densité de
, quelle est la densité de 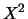 ?
Si
?
Si
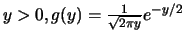 .
Si
.
Si
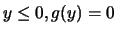 .
.
Vekemans
2002-06-24
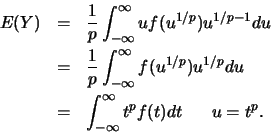
![\begin{eqnarray*}
E(Y)&=&\frac{1}{p} \int_{0}^{\infty} u [f(u^{1/p})+ f(-u^{1/p...
...t)]dt u=t^p\\
&=&\int_{-\infty}^{\infty} t^pf(t)dt.
\end{eqnarray*}](img603.png)
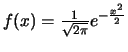 , quelle est la densité de
, quelle est la densité de